Parâmetros Adimensionais
Produzido por Giovanna RonzéTeoria
Introdução:
Na engenharia muitas vezes é interessante adimensionalizar as equações e combinar variáveis que formam números adimensionais. No estudo de convecção isso não é diferente, afinal é uma forma de reduzir o número total de variáveis.
Vamos dar uma olhada então e entender um pouco sobre alguns números adimensionais que vamos ver bastante em Convecção! Assim nos depararmos com eles nos próximos tópicos já vamos estar super familiarizados! Beleza?!
Número de Nusselt
O número de Nusselt é é um dos parâmetros adimensionais mais importantes. Ele é nada mais nada menos do que a forma adimensionalizada do coeficiente de transferência de calor por convecção , então, na prática ele vai ser muito usado para encontrar o valor de .
O número de Nusselt é dado pela seguinte expressão:
![]()
Onde é o comprimento característico e é a condutividade térmica do fluido. Observando a expressão para , vemos que ele é proporcional a , fisicamente isso significa que quanto mais eficiente for a transferência de calor por convecção, maior será o valor de .
Outro ponto importante é que, na expressão acima, o representa o coeficiente convectivo local, isso é, em um ponto específico do meu objeto. Em muitos momentos vai ser mais interessante trabalhar com o coeficiente convectivo médio . Então, seguindo o raciocínio da equação acima, podemos definir o número de Nusselt médio , calculado a partir de .
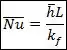
“Show de bola! Mas como fazemos pra calcular o número de Nusselt?!”

Então, não há uma equação apenas para calcular o número de Nusselt. Na real, existe uma série de equações, cada uma para um caso. Nós vamos chamar essas equações de correlações.
Para determinar qual correlação é a mais adequada, na maioria das vezes, nós vamos precisar de outros dois parâmetros adimensionais, o número de Reynolds e o número de Prandtl .
Nessas correlações, o número de Nusselt é sempre uma função tanto do número de Reynolds, quanto do número de Prandtl e, na maioria das vezes, possui a seguinte forma:
Como eu falei, essa é uma correlação geral, pode ser que você depare com algumas expressões um pouco diferentes. Mas fica tranquilo, expressões vão ser dadas, a medida que formos avançando na matéria!
Opa! Acho que está na hora de darmos uma atenção especial a esses dois novos parâmetros.
Número de Reynolds
Como vimos acima, é uma função do número de Reynolds , um outro parâmetro adimensional que vai ser muito importante pra a gente!
O número de Reynolds é um parâmetro adimensional que representa a razão entre as forças de inércia e as forças viscosas em um fluido. É ele quem nos diz se o escoamento em determinado ponto de uma superfície é laminar, turbulento. Como é dificil determinar em qual momento o escoamento deixa de ser laminar e passa a ser turbulento, definimos também uma zona de transição. Na prática, para efeitos de cálculo, definimos um ponto crítico onde o escoamento deixa de ser laminar.
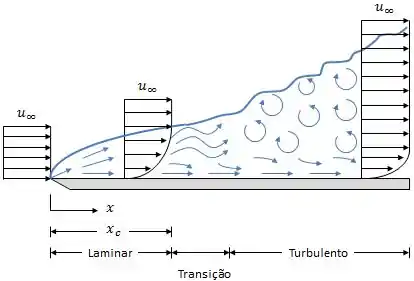
Saber se o escoamento é laminar ou turbulento é bem importante pra calcularmos o número de Nusselt.
Para placas planas, por exemplo, o número de Reynolds é calculado da seguinte forma:
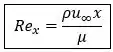
Sabendo que , substituindo, temos:
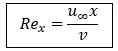
Onde:
- : Massa específica do fluido ;
- : Velocidade de corrente livre do fluido ;
- : Comprimento característico da placa ;
- : Viscosidade dinâmica do fluido ;
- : Viscosidade cinemática do fluido .
Para achar a posição termina o escoamento A zona de transição começa a partir de um ponto crítico , que podemos calcular a partir do número de Reynolds crítico .
Para problemas envolvendo placas planas, esse valor crítico é dado por:
![]()
Número de Prandtl
O número de Nusselt também é função do número de Prandtl (), isso significa que vamos precisar na hora de calcular . Então vamos falar um pouquinho dele também!
O número de Prandtl é a razão entre as difusividades de momento e térmica.
![]()
Na verdade, a gente nunca chega a ter que calcular o valor do número de Prandtl, porque ele é tabelado. Assim, na maioria dos exercícios, a primeira coisa que a gente faz é determinar as propriedades do fluido para uma temperatura de referência e, entre essas propriedades está o número de Prandtl. :)
Já estamos prontos pra partir pros exercícios!
Por fim, eu coloquei aqui um breve resumo de parâmetros adimensionais importantes em transferência de calor, alguns inclusive já trabalhados na parte de Condução.
Bônus: Outros Parâmetros Adimensionais
Vou te colocar de cara pro gol, se liga:
- Número de Prandtl :
- Número de Biot :
- Número de Fourier :
- Número de Nusselt :
- Número de Reynolds :
Razão entre as difusividades de momento e térmica.
![]()
Razão entre a resistência térmica de condução de um sólido e a resistência térmica de convecção na camada limite. Ele vai se muito utilizado nas questões de condução transiente!
![]()
Onde é a condutividade térmica do sólido.
Razão entre a taxa condutiva de calor e a taxa de armazenamento de energia térmica em um sólido. Ele corresponde ao parâmetro adimensional do tempo. E onde o tempo é muito importante? Justamente quando as nossas propriedades variam com ele! Ou seja, o número de Fourier vai ser usado nas questões de condução transiente!
![]()
Onde é a difusividade térmica.
Razão entre transferência de calor por convecção e somente por condução.
![]()
Onde é a condutividade térmica do fluido.
Razão entre as forças de inércia e as forças viscosas.
![]()
Número de Reynolds R e
Número de Prandtl P r
Bônus: Outros Parâmetros Adimensionais
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptada) Foram efetuados experimentos para determinar coeficientes de transferência de calor locais para o escoamento perpendicular a uma longa barra isotérmica de seção transversal retangular. A barra tem largura , paralela ao escoamento, e altura , normal ao escoamento.
Para números de Reynolds na faixa de , os números de Nusselt médios nas superfícies são correlacionados por uma expressão na forma
Os valores de e para a face frontal, faces laterais e face posterior da barra retangular foram determinados e são mostrados a seguir:

Determine o valor do coeficiente de transferência de calor de cada face da superfície exposta em um barra retangular com e .
A barra está exposta ao escoamento cruzado de ar com e .
Passo 1
Vamos nessa!
O problema já nos deu que:
Antes de qualquer coisa, vamos ver quais valores de e vamos usar pra resolver o problema.
Pra isso, de acordo com a tabela, precisamos calcular a razão , onde e .
Show de bola! Olhando agora pra tabela, vemos que, para :
- Face frontal: e ;
- Face lateral: e ;
- Face posterior: e ;
Passo 2
Outra coisa que vamos precisar para calcular o coeficiente convectivo é o número de Reynolds, dado por:
Então vamos aproveitar e buscar no livro todas as propriedades que vamos precisa pra resolver o problema. Pra isso, vou pegar aqui da tabela A.4 do Incropera os dados do ar a :
Voltando para o número de Reynolds:
Passo 3
Agora estamos prontos pra calcular o danado do Nusselt pra cada face, lembrando que:
Face frontal:
Face lateral:
Face posterior:
Passo 4
Agora é partir pro abraço e calcular os coeficientes convectivos, beleza?
Lembrando que:
Face frontal:
Face lateral:
Face posterior:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptada) Considere o escoamento de ar sobre uma placa plana com comprimento , sob condições nas quais a transição ocorre em baseada em um número de Reynolds críticos de .
Calculando as propriedades termofísicas do ar a , determine a velocidade do ar.
Nas regiões laminar e turbulenta, os coeficientes convectivos locais são, respectivamente,
Onde, em , , e possui unidade de .
Desenvolva uma expressão para o coeficiente convectivo médio, , como uma função da distância da aresta frontal, , para a região laminar, .
Desenvolva uma expressão para o coeficiente convectivo médio, , como uma função da distância da aresta frontal, , para a região turbulenta, .
Passo 1
Calculando as propriedades termofísicas do ar a , determine a velocidade do ar.
Pra começar, vamos pegar os dados do ar que vamos precisar para . De acordo com a tabela A.4 do Incropera:
Agora podemos continuar.
O número de Reynolds é dado por:
Sabemos que, para , . Dessa forma:
Passo 2
Desenvolva uma expressão para o coeficiente convectivo médio, , como uma função da distância da aresta frontal, , para a região laminar, .
Utilizando a definição do coeficiente convectivo médio, temos que:
Como, para o valor de que estamos interessados, o escoamento é exclusivamente laminar:
Substituindo a expressão de :
Onde .
Passo 3
Desenvolva uma expressão para o coeficiente convectivo médio, , como uma função da distância da aresta frontal, , para a região turbulenta, .
A ideia aqui é muito parecida com o que fizemos no passo anterior. A diferença agora é que, como , vamos ter que levar em consideração tanto a região laminar, quanto a turbulenta. Dessa forma, vamos ter o seguinte:
Como, para o valor de que estamos interessados, temos uma região laminar e uma região turbulenta:
Substituindo a expressão de e :
Onde , e . Logo:
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Resultados experimentais para a transferência de calor sobre uma placa plana com superfície extremamente rugosa puderam ser correlacionados por uma expressão com a forma
Onde é o valor local do número de Nusselt na posição , medida a partir da aresta frontal da placa.
Obtenha uma expressão para a razão entre os coeficientes de transferência de calor médio e local .
Passo 1
Vamos começar pelo coeficiente convectivo local .
Como já temos o número de Nusselt local, podemos associá-lo a através da seguinte equação:
Substituindo a expressão de , teremos:
Onde o número de Reynolds para uma placa plana é dada por:
Dessa forma:
Colocando um pouco de ordem na bagunça:
Passo 2
Por definição, o coeficiente convectivo médio será dado por:
Substituindo a expressão de que acabamos de encontrar:
Passo 3
Pra fechar, vamos calcular a razão :
Aqui podemos simplificar a maioria dos termos, só nos restando o seguinte:
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Ar forçado a e é usado para resfriar elementos eletrônicos em uma placa de circuito. Um desses elementos é um chip, que mede por , localizado a da aresta frontal da placa.
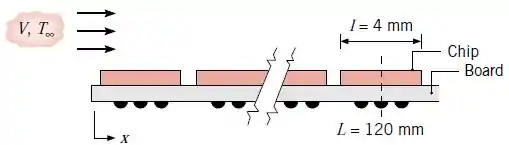
Experimentos revelaram que o escoamento sobre a placa é perturbado pelos elementos e que a transferência de calor por convecção é relacionada por uma expressão com a forma
Estime a temperatura superficial do chip se ele estiver dissipando .
Passo 1
Vamos nessa!
Podemos calcular a temperatura superficial do chip através da Lei de Resfriamento de Newton:
A única coisa que não temos dessa equação é justamente o coeficiente convectivo. Então vamos calcular esse cara.
Pra isso, antes de qualquer coisa, temos que encontrar as propriedades do ar que vamos precisar. Geralmente, nesse caso, a gente pega os dados a partir da média das temperaturas entre a da superfície e a de corrente livre .
Opa! Mas é justamente o cara que queremos calcular, como fazemos nesse caso?
Nesse caso, vamos ter que chutar um valor para , mas não pode ser nada absurdo aqui, beleza? Procure chutar um valor que vá ajudar na hora de olhar nas tabelas do livro.
Vamos chutar aqui um valor de . Fazendo isso, teremos:
Sendo assim, buscando os dados para , teremos o seguinte:
Agora podemos seguir em frente. :)
Passo 2
Pra calcularmos o coeficiente convectivo, vamos usar a equação de Nusselt que o problema nos deu:
Por definição:
Dessa forma:
Onde:
Substituindo os valores:
Passo 3
Agora podemos calcular a temperatura na superfície:
Onde:
Substituindo os valores:
Opa! O valor que encontramos foi bem próximo do valor que chutamos no início do problema, então esse foi um bom chute.
Caso os valores fossem muito distintos, a boa seria refazer os cálculos para um novo chute, agora mais próximo do valor que teríamos encontrado.
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
O desembaçador de pára-brisa de carros funciona jogando ar quente na superfície interna do pára-brisa. Para evitar a condensação de vapor d’água nesta superfície, a temperatura do ar e o coeficiente convectivo na superfície devem ser grandes o suficiente para manter uma temperatura na superfície , que seja, pelo menos, superior ao ponto de orvalho .
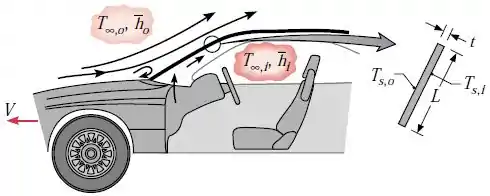
Considere um pára-brisa com comprimento e espessura , e condições de direção nas quais o carro se desloca a uma velocidade em um ambiente a .
Com base em experimentos de laboratório efetuados em um modelo do carro, sabe-se que o coeficiente de convecção médio na superfície externa do pára-brisa é correlacionado por uma expressão com a forma
, onde .
As propriedades do ar ambiente podem ser aproximadas por , e . Se e , qual é o menor valor de requerido para evitar a condensação na superfície interna?
Passo 1
O menor valor de será aquele para o qual a temperatura na superfície interna é igual à temperatura no ponto de orvalho, ou seja, .
Repare que o sistema dado pelo problema pode ser representado pelo seguinte circuito térmico:
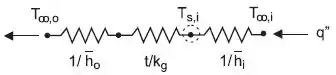
Como não temos o fluxo de calor no problema, podemos escolher um ponto e igualar o fluxo de calor calculado pelos dois lados desse ponto.
Nesse caso, vamos escolher a superfície interna do vidro, a qual sabemos a temperatura .
Dessa forma, a resistência térmica por unidade de área e o fluxo de calor à direita da superfície interna é dada por:
Do lado esquerdo, a resistência térmica por unidade de área e o fluxo de calor são dados por:
Onde é a condutividade térmica do vidro que, de acordo com a tabela A.3 do Incropera, vale .
Igualando as duas expressões do fluxo de calor, teremos:
Dessa expressão, a única coisa que não temos é o coeficiente convectivo externo . Então vamos trabalhar nesse cara.
Passo 2
De acordo com o problema, o coeficiente de convecção médio na superfície externa do pára-brisa é correlacionado por uma expressão com a forma
Por definição, o número de Nusselt médio é dado por:
Igualando as duas expressões:
Antes de continuarmos, vamos calcular esse número de Reynolds.
Passo 3
O número de Reynolds é dado por:
Onde:
Logo:
Passo 4
Voltando ao cálculo de :
Onde:
Substituindo os valores:
Agora podemos finalmente calcular ! Eu ouvi “amém”?! \o/
Passo 5
Voltando à expressão que encontramos no Passo 1:
Vamos reorganizar esse cada pra encontrar :
Onde:
Dessa forma:
