Introdução à Convecção
Teoria
Matando a saudade
Vamos dar um carinho especial à convecção a partir de agora!
“Pera aí! Que papo é esse?! Já trabalhamos com convecção antes!”
Bem lembrado! Lá em Condução nós cansamos de trabalhar com casos em que tínhamos troca de calor por convecção.
Nesses casos, vimos que o fluxo de calor por convecção entre a superfície de um corpo a uma temperatura e o ambiente, a uma temperatura , é dado pela Lei de Resfriamento de Newton, vamos matar a saudade dela:
Até aqui tudo bem!
“Mas o que temos que saber além disso sobre convecção?!”
Está vendo o termo da equação acima? Ele é o que chamamos de coeficiente de transferência de calor por convecção, ou coeficiente convectivo (esse nome é muito mais econômico, né?).
Acontece que, na maioria dos problemas em Condução, o valor de é dado no enunciado. Mas não é bem assim que as coisas acontecem na realidade.
Na realidade, o maior desafio na convecção é, justamente, determinar o coeficiente de transferência de calor por convecção .
Isso é um problema porque esse carinha depende de vários fatores como as propriedades do fluido, da geometria da superfície a qual o fluido está em contato e das condições do escoamento.
Camada-Limite Térmica
Se você já viu Mecânica dos Fluidos, esse nome talvez não lhe soe estranho. Nós vemos o conceito de camada-limite quando estudamos escoamentos de fluidos, e a ideia aqui é bem semelhante.
Uma camada-limite térmica se desenvolve toda vez que as temperaturas da corrente livre e da superfície são diferentes.
Vamos pensar em uma placa plana com temperatura uniforme . Antes de entrar em contato com a placa, todo o fluido possui uma mesma temperatura .
Mas, ao passar pela placa, as partículas em contato com a placa adquirem a mesma temperatura da placa. Essas partículas vão trocando energia com as camadas do fluido próximas, criando gradientes de temperatura no fluido.
Graficamente, acontece isso:
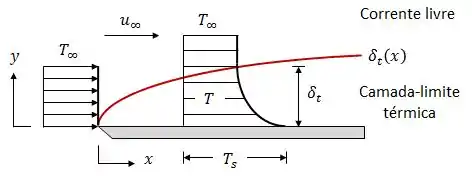
Nós definimos como camada-limite térmica a região onde está presente o gradiente de temperatura. A camada-limite térmica possui uma espessura , que é definida como o valor de para o qual:
Ou seja, a espessura da camada limite é definida pela região onde a diferença de temperatura entre a superfície da placa e do fluido vale da diferença entre a temperatura da superfície e a temperatura de corrente livre .
A camada-limite térmica tem uma cara muito parecida com a camada-limite de velocidade, se liga:
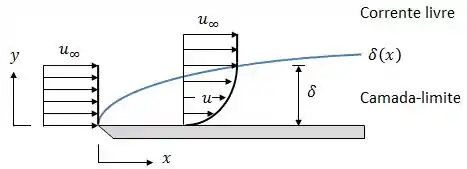
A diferença é que, quando olhamos para a velocidade, vemos que as partículas em contato com a placa possuem velocidade nula, essas partículas vão desacelerando as camadas de fluido próximas, e assim por diante.
O resultado é o gradiente de velocidade mostrado acima.
Como isso influencia no valor de ?!
Como acabamos de ver, o fluido em contato com a superfície da placa possui velocidade nula, ou seja, significa dizer que, nessa camada de espessura infinitesimal o calor é transferido somente por condução, dessa forma:
Onde corresponde à condutividade térmica do fluido.
Se igualarmos esse expressão à expressão da Lei de Resfriamento de Newton, teremos o seguinte:
Se dermos um jeitinho na bagunça:
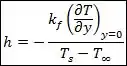
CALMA! Não decore essa expressão, vamos analisá-la pra entender como a camada-limite térmica influencia no valor de , beleza?
Se liga que os valores de , e são constantes. Então só teremos que olhar com carinho pro gradiente de temperatura .
Vamos olhar pra essa imagem novamente:
Conforme vamos aumentando o valor de , teremos a seguinte sucessão de eventos:
- Conforme o valor de aumenta, a espessura da camada-limite térmica também aumenta;
- O aumento da espessura irá diminuir o gradiente de temperatura ;
- A redução do gradiente de temperatura irá diminuir o coeficiente convectivo ;
- Se o coeficiente convectivo diminuir, o fluxo de calor também irá diminuir.
Conclusão, e diminuem com o aumento de .
Então tenho que conhecer o coeficiente convectivo em cada ponto?!
Quase isso!
Há duas formas de tratarmos o coeficiente convectivo: através de seu valor local, ou através de seu valor médio.
Coeficiente Convectivo Local
Vamos supor que a gente conheça o coeficiente convectivo local e, por consequência, o fluxo de calor local . Nesse caso, pra calcularmos a taxa total de transferência de calor , teríamos que calcular a seguinte integral:
Onde corresponde à área da superfície.
Substituindo a expressão do fluxo de calor:
Coeficiente Convectivo Médio
Outra forma de calcular essa mesma taxa de transferência de calor é através do coeficiente convectivo médio, definido por:
Para os casos em que depende somente da distância , podemos escrever a equação acima da seguinte forma:
Utilizando esse valor médio, a taxa de transferência de calor pode ser escrita da seguinte forma:
Temperatura de Filme
Esse é apenas um detalhe desse capítulo, mas isso é MUITO IMPORTANTE!
Acontece que, na maioria dos casos, vamos ter que determinar as propriedades do fluido para resolver um problema (a não ser o enunciado nos dê os valores de mão beijada).
Os valores dessas propriedades estão todas tabeladas em função da temperatura. Assim, precisamos de uma temperatura de referência pra pegar os dados na tabela. Essa temperatura de referência é a temperatura de filme , dada por:
Onde é a temperatura da superfície em contato com o fluido e é a temperatura de corrente livre.
Agora sim! Partiu exercícios?! Responde Aí! ;)
Camada-Limite Térmica
Como isso influencia no valor de h ?!
Então tenho que conhecer o coeficiente convectivo em cada ponto?!
Temperatura de Filme
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Água a uma temperatura de escoa sobre uma das superfícies de uma parede de aço (AISI 1010), cuja temperatura de . A parede possui uma espessura de e sua outra superfície está a uma temperatura de .
Para condições de regime estacionário, qual é o coeficiente convectivo associado ao escoamento da água?
Quais são os gradientes de temperatura na parede e na água que está em contato com a parede?
Esboce a distribuição de temperaturas na parede e na água a ela adjacente.
Passo 1
Antes de qualquer coisa, precisamos das propriedades de cada material envolvido no problema.
Para o aço (AISI 1010), as propriedades serão tomadas na temperatura média entre as superfícies:
De acordo com a tabela A.1 do Incropera (fazendo uma interpolação linear), encontramos que .
Para a água, vamos buscar as propriedades de acordo com a temperatura média entre a de escoamento livre e a da placa em contato com o fluido. Logo:
De acordo com a tabela A.6 do Incropera .
Agora podemos seguir em frente.
Passo 2
Para condições de regime estacionário, qual é o coeficiente convectivo associado ao escoamento da água?
A ideia do problema é essa aqui:
Como estamos trabalhando com regime permanente, o fluxo de calor por condução que chega à superfície de deve ser igual ao fluxo de calor por convecção que é transferido da mesma para a água. Logo:
Reorganizando os termos:
Substituindo os valores:
Passo 3
Quais são os gradientes de temperatura na parede e na água que está em contato com a parede?
Quando falamos em gradiente de temperatura, estamos falando na Lei de Fourier, logo, para a parede:
Já para a água em contato com a parede, temos que:
Passo 4
Esboce a distribuição de temperaturas na parede e na água a ela adjacente.
A temperatura varia linearmente no interior do aço mas quando passa para o fluido, a temperatura se comporta de maneira diferente, assim, como vimos na Teoria. Logo, a distribuição de temperatura vai ter essa cara:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Para o escoamento laminar sobre uma placa plana, sabe-se que o coeficiente de transferência de calor local varia com , onde é a distância da aresta frontal da placa.
Qual é a razão entre o coeficiente médio entre a aresta frontal e alguma posição na placa e o coeficiente local em ?
Passo 1
Vamos começar olhando para o coeficiente convectivo médio em um ponto qualquer.
Como o coeficiente convectivo depende somente da distância , podemos calculá-lo da seguinte forma:
O problema nos diz que varia com , então vamos escrevê-lo como:
Onde é uma constante qualquer. Voltando para o cálculo de , teremos:
Passo 2
Com relação ao coeficiente convectivo local, temos que:
Dessa forma, calculando a razão entre os dois:
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
O escoamento paralelo de ar atmosférico sobre a superfície de uma placa plana de comprimento é perturbado por uma série de bastões estacionários posicionados na trajetória do escoamento sobre a placa.
Medidas em laboratório do coeficiente convectivo local na superfície da placa foram efetuadas para um dado valor de e . Os resultados são correlacionados por uma expressão na forma , onde possui unidades de e está em metros.
Calcule o coeficiente convectivo médio sobre toda a placa e a razão na aresta traseira .
Passo 1
Por definição, como varia somente com , o coeficiente convectivo médio de toda a placa será dado por:
Substituindo a expressão de :
Integrando a expressão acima:
Substituindo os limites de integração:
Onde , logo:
Passo 2
O coeficiente convectivo local aresta traseira será dado por:
Onde , logo:
Passo 3
Finalmente, calculando a razão :
Opa! “Então quer dizer que esses caras serão sempre iguais?!”
NÃAAAAAO! Foi só uma coincidência desse problema, ok?! :)
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Ar com uma temperatura na corrente livre de , escoa paralelamente sobre uma placa plana de comprimento e temperatura .
Entretanto, obstáculos colocados no escoamento intensificam a mistura com o aumento da distância da aresta frontal e a variação espacial das temperaturas medidas no interior da camada-limite é correlacionada por uma expressão da forma onde e representam respectivamente os eixos horizontal e vertical, e estão em metros.
Determine e represente graficamente a maneira pela qual o coeficiente convectivo local varia com . Calcule o coeficiente convectivo médio para a placa.
Passo 1
Por definição, o coeficiente convectivo é dado por:
Opa! Antes de continuarmos precisamos saber quanto vale a condutividade térmica do ar nessas condições.
Para pegar o valor de , utilizaremos a temperatura média entre a de corrente livre e a da superfície da placa .
De acordo com a tabela A.4 do Incropera (e fazendo uma interpolação linear), encontramos que .
Passo 2
Voltando para a expressão de :
Onde:
Temos que:
Passo 3
Graficamente, o coeficiente convectivo irá variar linearmente com , de acordo com a função que encontramos no passo anterior.
Para (aresta traseira da placa), . Dessa forma:
Passo 4
Pra fechar, temos que calcular o coeficiente convectivo médio. Pra isso, como o mesmo varia somente com , basta utilizar a expressão:
Substituindo os limites de integração:
Onde , logo:
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
A taxa de transferência de calor, por unidade de largura (normal à página), em uma seção longitudinal,, , pode ser representada por , onde é o coeficiente médio na seção de comprimento .
Considere escoamento laminar sobre uma placa plana com uma temperatura uniforme . A variação espacial do coeficiente convectivo local tem a forma , onde é uma constante.
Partindo da equação da taxa convectiva na forma , deduza uma expressão para em termos de , e .
Deduza uma expressão para em termos de , e dos coeficientes médios e , correspondentes aos comprimentos e respectivamente.
Passo 1
Partindo da equação da taxa convectiva na forma , deduza uma expressão para em termos de , e .
Beleza, temos que partir dessa equação aqui:
Se integrarmos esse cara entre os pontos e (que estamos interessados), encontraremos o seguinte:
Ao mesmo tempo, o próprio enunciado, como quem não quer nada, nos disse que:
Opa! Se igualarmos essas duas expressões, teremos que:
Reorganizando os termos:
No próximo passo, vamos partir pra integração desse cara.
Passo 2
Segundo o enunciado, . Substituindo isso na expressão de :
Agora é só integrar e arrumar a casa:
Finalmente:
Passo 3
Deduza uma expressão para em termos de , e dos coeficientes médios e , correspondentes aos comprimentos e respectivamente.
Então, nós podemos resolver essa questão de duas formas: calcular , e relacioná-los com , ou utilizar a própria o conceito da taxa de transferência de calor dada pelo problema.
Os coeficientes médios e serão dados por:
Agora o nosso objetivo é encaixar esses dois caras na expressão de que encontramos no passo anterior.
Pra isso, vamos isolar as raízes em cada expressão, ok?
Substituindo na expressão de , teremos:
Organizando a bagunça, teremos que:
Resposta