O desembaçador de um carro funciona jogando ar quente na superfície interna do para-brisa. Para evitar a condensação de vapor d’água nesta superfície, a temperatura do ar e o coeficiente convectivo na superfície devem ser grandes o suficiente para manter uma temperatura na superfície que seja, pelo menos, superior ao ponto de orvalho .
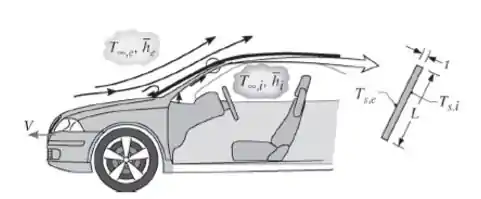
Considere um para-brisa com comprimento e espessura , e condições de direção nas quais o carro se desloca a uma velocidade de em um ar ambiente a . Com base em experimentos de laboratório efetuados em um modelo do carro, sabe-se que o coeficiente de convecção médio na superfície externa do para-brisa é correlacionado por uma expressão com a forma , com . As propriedades do ar podem ser aproximadas por , e . Se e , qual é o menor valor de requerido para evitar a condensação na superfície interna?
Passo 1
Primeiramente desenharemos o circuito térmico melhor analisarmos o problema:
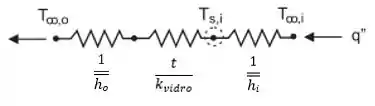
Passo 2
Realizando um balanço de energia, temos que:
Esses dois termos apresentados podem ser escritos como:
E
Igualando as equações:
Rearranjando, temos:
Passo 3
A relação para o número de Nusselt apresentada no enunciado é:
Sendo:
Temos:
Isolando :
Dados:
;
;
;
;
.
Temos:
Passo 4
Voltando na equação do Passo 2:
Dados:
;
;
;
;
.
Temos: