Força em Comportas
Produzido por Raphael EloiTeoria
Lembra que você descobriu que fazer cerveja era a profissão da sua vida?
Na primeira teoria você descobriu que ama fazer cerveja e resolveu fazer isso da vida. Pois bem, após algumas cervejas produzidas e muito dinheiro o tanque que armazenava a cerveja rachou. Você cortou o pedaço rachado e pretende colocar uma chapa no lugar. Pois bem, você pode colocar qualquer chapa? Quais são as forças que essa chapa tem que resistir?
Esse é seu recipiente furado:
![]()
Que ao colocarmos uma chapa retangular para arrumar o buraco e podermos preencher de cerveja, pode ser esquematizado assim:
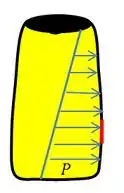
Em vermelho a chapa que tampa o furo, o amarelo é a cerveja e em azul o comportamento da pressão devido à cerveja, certo? Quanto mais fundo maior a pressão.
Mas e ae como descobrir o quanto essa pressão vai gerar de força na chapa? E onde seria aplicada essa força? No centro de gravidade da placa?
É isso que vamos aprender a responder nessa teoria.
Começaremos aprendendo a descobrir a força gerada pela pressão hidrostática em uma chapa.
Na verdade não é aprender e sim relembrar, pois já vimos isso em resistência do material.
Lembra quando você tinha uma viga e sobre ela um carregamento? Tipo assim:
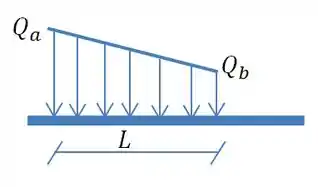
Bem, no nosso caso a gente tem a seguinte configuração.
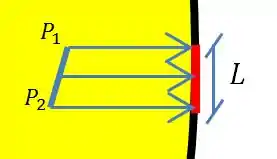
Onde e E a área da nossa chapa é
OBS: Observe que nas pressões não levem em conta a pressão atmosférica. Bem, é porque ela atua em cima da cerveja e fora do tanque, então ela se anula. Isso geralmente vai ocorrer, só não irá se algum dos lados for tampado. Então preste atenção nisso para considerar ou não a pressão atmosférica.
Para encontrar a força atuante na placa iremos encontrar a pressão média na placa e depois multiplicar essa pressão pela área da placa, pois .
Para encontrar a pressão média é simples, basta somar as pressões nos extremos e dividir por 2, já que a pressão varia linearmente.
Então vamos ter que:
Como estamos estudando apenas placas planas, o centro de gravidade de uma placa plana homogênea é sempre metade de seu comprimento, ou seja, no seu centro geométrico (conhecido também como centroide). Sendo assim, podemos entender que:
Assim, chegamos na equação que vamos usar para calcular a força exercida por uma pressão em qualquer placa plana submersa em um fluido.
Esse termo nada mais é do que a pressão no centro de gravidade da placa .
Isso serve para qualquer placa plana homogênea que você for utilizar, não importa se é um triângulo, quadrado ou círculo.
Metade do problema já foi, agora precisamos apenas descobrir onde essa força será aplicada.
Eu havia perguntado se seria no centro de gravidade assim como a força peso. Vamos ver se faz sentido?
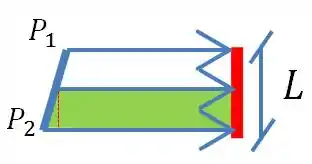
Olhando para o sistema que esquematizamos, a parte em verde representa uma maior pressão que a em branco. O que nos mostra que a parte de baixo da chapa é submetida a uma pressão bem maior que a de cima, será que poderíamos representar a força resultante dessa pressão no meio da chapa?
Não, né?! Se a parte de baixo é submetida a maior pressão e tem a mesma área que a parte de cima, então a força exercida em baixo é maior que a em cima, assim ao representar a força resultante no centro de gravidade estaríamos cometendo um grande erro.
O ponto de aplicação dessa força é o chamado, centro de pressão.
E as coordenadas dele são:
Vamos explicar o que é cada termo agora.
1- é o peso específico do fluido em questão.
2- é o ângulo que a placa faz com a horizontal.
3- é a força que acabamos de calcular, podemos escrever como também.
4- A integral, parte louca, que ninguém gosta. Bem, essa é a parte que temos que tratar com carinho. Bem, essa integral é o momento de inércia da chapa.
No primeiro, caso o momento de inércia em relação ao eixo calculado no plano da placa. Por isso podemos escrever assim a fórmula para encontrar a coordenada
E na coordenada a integral corresponde ao momento de inercia . Assim,
Então no caso do nosso exemplo. A coordenada é , pois é um retângulo e é simétrico nessa direção.
Já é
Podemos cortar com o que são a mesma coisa.
E então chegamos em:
Bem, o momento de inércio de um retângulo é
Lembrando que a área da nossa placa é , então a nossa coordenada é:
Importantíssimo: As coordenadas e que calculamos são em relação ao centro de gravidade da placa. Assim, se encontramos e o centro de gravidade da peça está em , significa que a posição do centro de pressão é . E o sinal negativo significa que está para baixo ou a esquerda do centro de gravidade. Então se o centro de pressão está abaixo do centro de gravidade e se o centro de pressão está à esquerda do centro de gravidade.
Mas para que saber a posição de aplicação dessa força? Lembra dos exercícios de estática que tínhamos um objeto, várias forças e o problema pedia qual era a força em uma posição aleatória que manteria o sistema em equilíbrio?
Bem, muitos dos exercícios que você verá daqui para a frente abordarão uma represa, a comporta da represa e lhe fará perguntas desse tipo, qual a força nesse ponto para que a comporta não abra.
Então, não se esqueça de considerar a força de pressão que acabamos de aprender como encontrar, a força peso e a força de reação se tiver algum apoio.
Ahh, e na estática trabalhamos sempre com a ajuda de duas equações:
Além disso, vale relembrar o momento de inércia do círculo, triangulo e retângulo. E suas respectivas áreas também.
Fluido dos dois lados
Vimos o caso em que temos fluido de um lado e o outro lado está sujeito apenas a pressão atmosférica.
Mas o que acontece se tivermos uma coluna de fluido do outro lado também? Como na figura abaixo:
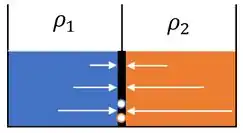
Vai rolar que irá surgir uma força de pressão do outro lado, aplicada em um outro centro de pressão (representados pelos pontos na comporta). As formulas para calcularmos isso continuam sendo as mesmas.
O que vai acontecer é que agora temos mais uma força e mais um ponto de aplicação que devemos levar em conta quando formos montar a equação de momento ou de força. 😉
É isso galera, a matéria consiste em encontrar a força e a o centro de pressão, porém as questões vão abordar parte de estática, trigonometria e outras matérias. Então vamos aos exercícios treinar e pegar o jeito dessas questões.
Fluido dos dois lados
Exercícios Resolvidos
Exercício Resolvido #1
Explique e diferencie o centro de pressão e centróide.
Passo 1
Vamos começar falando de centróide ou centro geométrico, que é algo nada novo para gente.
Centróide é o ponto que representa que dividindo o corpo naquele ponto você terá igualdade de área se for um centroide de área, de volume se for um centroide de volume.
Quando temos um corpo homogêneo o centroide coincide com o centro de gravidade representando assim o ponto de aplicação da força Peso .
Já o centro de pressão representa o ponto em que é aplicado a força causada pela pressão de um fluido. Como já vimos a pressão não é constante ao longo do comprimento do fluido e por isso não faz sentido ser aplicada no centroide.
Resposta
Centróide ponto de aplicação da força peso e centro de pressão ponto de aplicação da força de pressão.
Exercício Resolvido #2
Um tanque de água tem uma comporta em sua parede vertical com de altura e de largura. O topo da comporta está abaixo da superfície. Qual é a força hidrostática sobre a comporta? E a que distância abaixo da superfície está o centro de pressão da força hidrostática?
Passo 1
Bem, queremos saber a força hidrostática sobre a comporta. Vimos na teoria que a fórmula para isso é:
E a pressão no centro de gravidade é dada por:
Onde representa a profundidade do centro de gravidade.
No nosso caso sabemos que o centro de gravidade da comporta está no meio dela:
Como queremos a profundidade, então temos:
Já que temos dois metros de água acima da comporta.
Assim, a força hidrostática na comporta é:
A área da comporta é simples, pois ela é um retângulo.
Como o líquido tratado é água e a densidade foi dada como que é igual a
Assim, a força hidrostática é:
Passo 2
Agora queremos descobrir a posição do centro de pressão.
Vimos na teoria que a posição vertical do centro de pressão é dada por:
Cortando a densidade mássica e substituindo por , que é o ângulo que a comporta faz com a horizontal, temos:
Lembrando que o momento de inércia de uma chapa retangular é:
Substituindo isso, temos:
Bem essa posição é em relação ao centro de gravidade, então para acharmos essa posição em relação a superfície devemos fazer:
Resposta
Exercício Resolvido #3
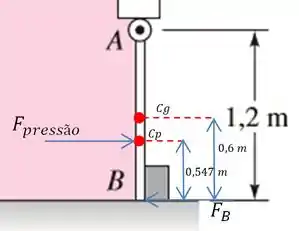
A comporta na Figura abaixo tem de largura, está articulada em e limitada por um limitador em . A água está a . Calcule a força no limitador e as reações em A se a profundidade da água é
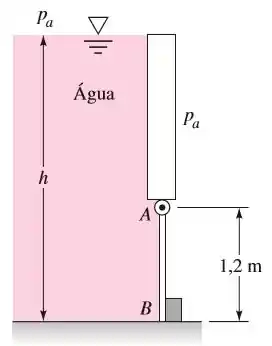
Passo 1
Para resolvermos esse item precisamos descobrir o valor da força causada pela pressão de água na comporta, no ponto onde essa pressão está sendo aplicada, . E após isso, vamos usar o fato dela estar parada para descobrir a força aplicada no limitador . Para isso vamos usar:
Como disse teremos a atuação da força de pressão no centro de pressão () e da força no limitador impedindo que a comporta abra.
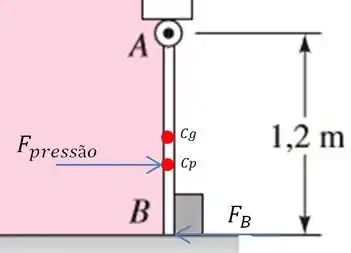
Montando a equação de momento em relação ao ponto , temos:
Lembrando que as distâncias são em relação ao ponto . E por isso fizemos a gente já tem .
E por isso para resolvermos o problema basta descobrirmos a força de pressão e a posição do centro de pressão.
Passo 2
Já sabemos como resolver, agora só falta atacar mesmo né?!
Na teoria vimos que a força de pressão é dada por:
A densidade da água a a gente sabe que é . A aceleração da gravidade é . E a profundidade do centro de gravidade a gente tem que calcular.
O centro de gravidade de uma chapa retangular fica bem no meio, assim a posição do centro de gravidade em relação ao fundo, ponto , é:
Mas a gente quer a profundidade e por isso temos que fazer a profundidade total do fluido menos a posição do centro de gravidade em relação ao fundo.
E por fim vamos calcular a área da comporta.
Podemos então calcular a força de pressão na comporta.
Passo 3
Agora vamos encontrar a posição do centro de pressão. Bem, estamos interessados só na posição , pois é dela que precisamos para aplicar a equação de momento.
Assim, na teoria vimos que a fórmula para encontrar o centro de pressão em relação ao centro de gravidade é:
O ângulo que a placa faz com a horizontal é e é
A força de pressão a gente já calculou. Por fim falta apenas o momento de inércia da placa. Como é uma placa retangular o momento de inércia é:
A base é a largura, que vale . A altura também foi dada e vale . Assim o momento de inércia é:
Jogando isso tudo na fórmula temos:
Lembrando que isso é em relação ao centro de gravidade, o que significa que a posição do centro de pressão é:
Então ficamos assim:
Beleza, agora podemos voltar para a equação do momento, lembrando que as distâncias devem ser em relação ao ponto .
Isolando , temos:
Passo 4
Agora queremos a reação em A.
O jeito mais fácil de fazer isso é usando o fato que para estar parado o somatório de força tem que ser zero.
As forças atuantes são: A força de reação , a força de pressão e a força de reação . Assim, temos que:
Isolando , temos:
Já encontramos o valor das duas forças, então basta substituir
Vale ressaltar que não temos a atuação de forças na direção do eixo , que é na direção da largura da comporta, por isso a reação nessa direção é zero. .
Resposta
Exercício Resolvido #4
Uma comporta plana semicircular , articulada ao longo de , é suportada pela força horizontal aplicada em . O líquido à esquerda da comporta é água. Calcule a força requerida para o equilíbrio.
Dados:
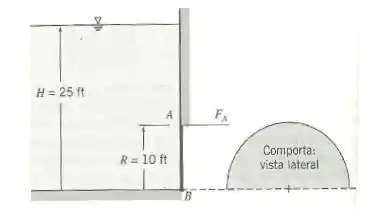
Passo 1
Essa questão é muito parecida com a anterior, o que vai mudar é que a comporta não é retangular. E isso vai influenciar na posição do centro de gravidade e no momento de inércia e, assim, mudar muitos valores. Mas o raciocínio para resolver é o mesmo.
Para resolvermos precisamos descobrir o valor da força causada pela pressão de água na comporta e o centro de pressão para podermos aplicar a equação de momento.
Passo 2
Vamos começar descobrindo a força de pressão.
Na teoria vimos que a força de pressão é dada por:
A densidade da água a gente sabe que é . A aceleração da gravidade é . E a profundidade do centro de gravidade a gente tem que calcular.
Para usarmos tudo em vamos transformar os valores que temos:
E:
Continuando agora, vamos calcular o centro de gravidade.
Bem, pra um semicírculo, o centro de gravidade é:
Mas a gente quer a profundidade e por isso temos que fazer a profundidade total do fluido menos a posição do centro de gravidade em relação ao fundo.
E por fim vamos calcular a área da comporta.
Podemos então calcular a força de pressão na comporta.
Passo 3
Agora vamos encontrar a posição do centro de pressão. Bem, estamos interessados só na posição , pois é dela que precisamos para aplicar a equação de momento.
Assim, na teoria vimos que a fórmula para encontrar o centro de pressão em relação ao centro de gravidade é:
O ângulo que a placa faz com a horizontal é e é:
A força de pressão a gente já calculou. Por fim falta apenas o momento de inércia da placa. Como é uma placa semicircular, o momento de inercia dessa figura:
Atenção. Aqui usamos o momento de inércia xx, que é o momento de inércia relativo à rotação em torno do eixo paralelo ao x que passa pelo centro de gravidade.
O Raio nós temos, então:
Jogando isso tudo na fórmula temos:
Lembrando que isso é em relação ao centro de gravidade, o que significa que a posição do centro de pressão é:
Então ficamos assim:
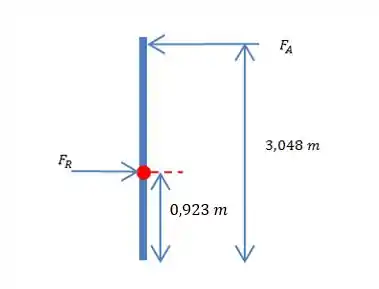
Beleza, agora podemos escrever a equação de momento, lembrando que as distâncias devem ser em relação ao ponto .
Isolando , temos:
Resposta
Exercício Resolvido #5
Determinar o mínimo valor de , para o qual a comporta da figura girará em torno do ponto O, se a comporta é retangular de de largura. Dado .
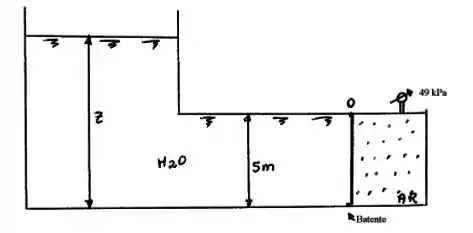
Passo 1
Essa questão é parecida com as que já fizemos, mas ela tem um detalhe muito importante.
Lembra na teoria quando falamos que estávamos desconsiderando a pressão atmosférica, pois ela estaria na maioria das vezes aplicada aos dois lados?
Pois bem, nesse caso a gente continua tendo a aplicação da pressão atmosférica dos dois lados.
Porém do lado externo da comporta existe uma pressão extra a da atmosférica, que o manômetro está medindo que vale .
Então vamos continuar ignorando a pressão atmosférica, mas temos que agora levar em conta a pressão do lado externo.
OBS: Observe que no lado externo temos a aplicação da pressão atmosférica mais a pressão do ar que vale . Por isso podemos não considerar a pressão atmosférica, pois ela atua tanto no lado externo quanto interno.
Bem, vamos começar a resolver o problema. Como temos pressão dos dois lados, teremos força atuando dos dois lados.
Existem duas maneiras da comporta se mexer uma é se e a outra se
Vamos primeiro começar pelo somatório de força.
Como vimos com a pressão atmosférica que a pressão de um lado anula a do outro. Podemos observar que a comporta vai começar a se mexer quando a pressão da coluna de liquido no centroide superar a pressão de ar no lado externo.
Assim, quando:
Já que para os dois lados a área da chapa é a mesma.
Então basta resolvermos a inequação:
Para descobrirmos o valor de .
Bem, dado que é uma comporta retangular o centro de gravidade é na metade do comprimento, assim valendo .
Como queremos a profundidade do centro de gravidade, basta fazer:
Tendo e sabendo a densidade mássica da água, podemos substituir os valores na inequação:
Então, chegamos que em:
Passo 2
Agora, vamos começar a analisar a segunda opção
Para essa opção vamos ter que encontrar o ponto de aplicação das duas forças.
Vamos começar com a força externa, como a pressão no lado externo é constante então o ponto de aplicação é no centro de gravidade.
Sendo assim o ponto estaria a do ponto .
E a força aplicada nesse ponto seria:
Agora vamos analisar a região interna, a força vai ser dada em função de .
E o ponto de aplicação será o centro de pressão que é calculado por:
Podemos simplificar já que o ângulo que a comporta faz com a horizontal é .
A área já sabemos que é a profundidade do centro de gravidade também já conhecemos,
Só falta o momento de inércia, esse a gente tem que calcular:
Substituindo, temos:
Esse valor é em relação ao centro de gravidade, queremos o valor em relação ao fundo. Dessa força a coordena do centro de pressão é:
Agora, temos que montar a equação de momento.
Como estamos analisando o momento em que ela começa a se mexer, ou seja, o momento em que a comporta perde contato com o batente, a força nesse ponto é zero.
Vamos fazer o momento em relação ao ponto , assim agindo apenas duas forças a força interna e a força externa.
Feia, né? Vamos começar simplificando ela: Primeiro vamos fazer a multiplicação
Podemos dividir a equação por 2,5 e por 10.000 e assim teremos:
Agora, vamos dividir a equação por 9,8 e vamos obter:
E por fim, basta isolar , que encontramos:
Como queríamos o menor valor de que faça a comporta se movimentar, o menor valor é .
Resposta
Exercício Resolvido #6
Encontre a linha de ação e o valor da força no portão circular da figura:
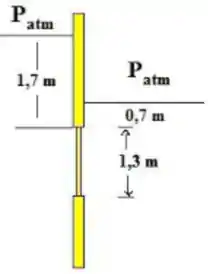
Passo 1
Agora, ao invés de termos um pressão fixa do lado externo igual na questão anterior, teremos de ambos os lados forças devido pressão causada pela coluna de fluido.
Para encontrarmos a força resultante basta primeiro encontrarmos a pressão resultante no centro de gravidade.
Assim, temos que
Encontrando a pressão resultante no centro de gravidade encontramos a força resultante.
A pressão no centro de gravidade é dada por:
O fluido é o mesmo dos dois lados. Assim o que vai influenciar diferenciar a pressão interna da externa será a profundidade do centro de gravidade.
Vamos começar calculando a pressão do lado esquerdo, região interna.
Como é uma placa plana e circular o centro de gravidade se encontra no meio da placa. Assim em .
Beleza, encontramos a pressão na região interna:
Já a pressão no lado direito será:
Agora vamos ver qual é a pressão resultante.
Como queremos a força, basta multiplicar pela área do portão. Tendo assim:
Passo 2
Beleza, agora vamos encontrar a linha de ação dessa força resultante. Mas pera!, o que seria a linha de ação de uma força??
Bem, é onde a força estaria virtualmente atuando, como se fosse o ponto onde aplicaríamos essa força resultante.
Por que isso? Bem, a força do lado esquerdo vai ser aplicada em um centro de pressão e a do outro lado será aplicada em outro centro de pressão.
E para gente achar o centro de pressão resultante teremos que fazer uma média ponderada com os centros de pressões onde os pesos serão as forças.
Estranho né? Vamos resolver o problema que você vai entender melhor.
Precisamos encontrar os centros de pressão de cada força.
Começando pelo lado esquerdo, temos:
Substituindo os valores que temos, chegamos em:
Olhando naquela tabela da teoria vemos que para um círculo:
Dessa forma:
Agora faremos o mesmo para encontrar o centro de pressão da pressão à direita.
Então chegamos na seguinte solução:
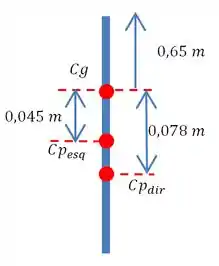
Bem, agora temos que encontrar a posição média do centro de pressão resultante. E para isso vamos fazer uma média ponderada. Onde o peso é a força em cada centro de pressão:
Usaremos o módulo das forças. E assim, temos:
Como essa posição representa um ponto abaixo do centro de gravidade deve ser colocado o sinal de negativo antes, sendo assim a posição em relação ao centro de gravidade:
Assim, temos que a força resultante irá aturar na posição:
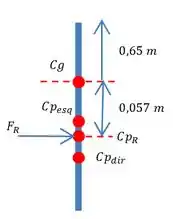
Resposta
Exercício Resolvido #7
Um portão plano, de espessura uniforme, suporta água a uma certa profundidade, como abaixo. Encontre o peso mínimo que o portão deve ter para que permaneça fechado.
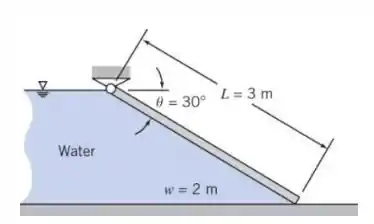
Passo 1
Agora, temos uma comporta inclinada. Sendo assim, o peso da comporta deve ser levado em conta.
O peso atua no centro de gravidade. Vamos posicionar a força peso. E decompô-la. Assim,
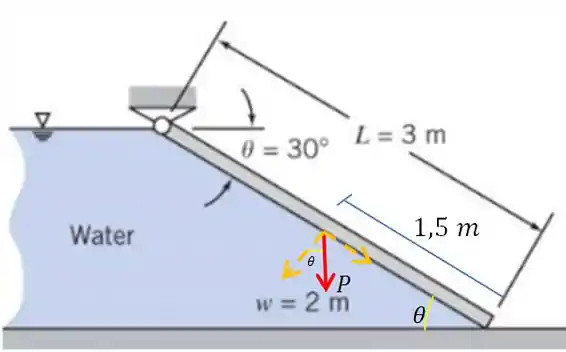
A componente que do peso que vai importar para gente é a componente perpendicular ao portão. Então lembrando daquela regrinha de decomposição. “Co-lado/Se-parado” Como queremos a componente colada com o ângulo, vamos usar o cosseno.
Assim,
Agora, falta apenas encontrarmos a força causada pela coluna de água.
Para isso vamos usar as fórmulas que aprendemos:
A densidade mássica da água a gente já viu que vale:
A profundidade do centro de gravidade a gente tem que calcular.
Bem, o que a gente tem é mais ou menos isso:
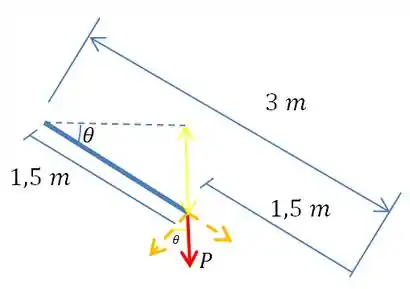
Beleza, para descobrir a profundidade do centro de gravidade, a gente vai usar a seguinte relação:
Assim,
A área do portão é só multiplicar o comprimento pela largura:
Assim, a força de pressão é:
E o centro de pressão é:
Temos quase tudo, só falta calcular o momento de inércia.
Como a placa é retangular o momento de inércia é dado por:
Agora, podemos calcular a posição do centro de pressão:
Agora, temos todas as posições e forças. Ficamos com um esquema assim:
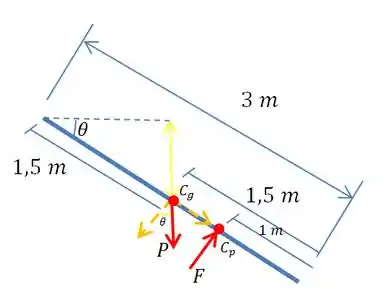
Então podemos aplicar a equação de momento. Faremos o momento em relação ao ponto de rotação do portão, isto é o pino dele. Lá em cima.
Se o peso for menor que isso o momento não será zero o que significará que o portão entrará em movimento.
Resposta
Exercício Resolvido #8
Determine a força e seu ponto de aplicação para a comporta da figura. A substância de trabalho é a água. (Este exercício exige um bom conhecimento da teoria).
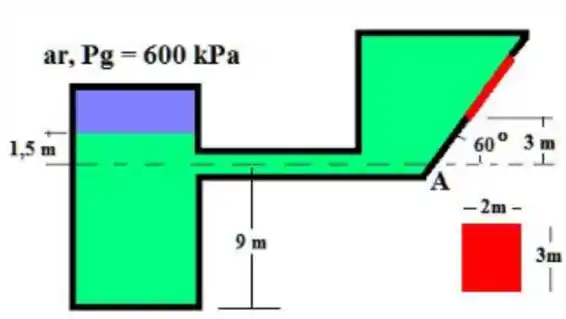
Passo 1
Queremos saber a força aplicada na comporta e o ponto de aplicação, certo?
A pressão a gente viu que é:
Mas ae que vem o diferente dessa questão, a gente não tem ideia dá altura do tanque em que a comporta está localizada.
E para descobrir essa altura vamos usar o que vimos na teoria de vasos comunicantes. Lembra que dois pontos no mesmo fluido tem a mesma pressão?
Então, vamos usar isso para descobrir a altura no tanque a direita analisando esses dois pontos:
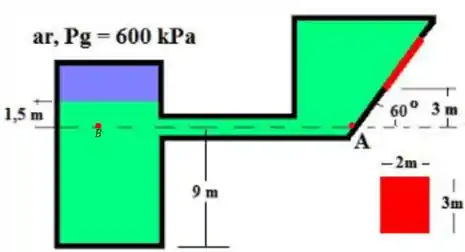
A pressão do lado esquerdo, ponto , é dada pela pressão e pela pressão da coluna de liquido , assim
Já a pressão no ponto é dada apenas pela coluna de liquido, sendo assim
Como , então vamos igualar as pressões e descobrir a profundidade do tanque a direita.
Então, temos a seguinte configuração:
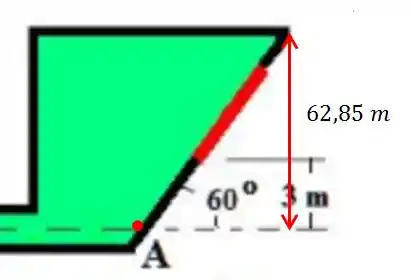
Agora falta apenas descobrirmos a posição do centro de gravidade. Vamos dar um zoom na parte da comporta e olhar só para ela. Vamos ter a seguinte configuração:
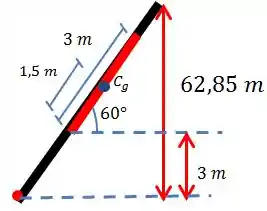
Com isso, usando a relação de
Assim, descobrimos que
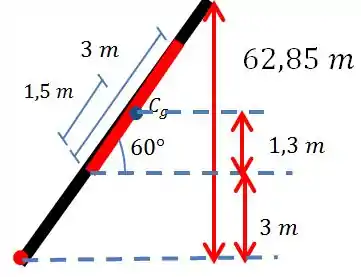
Agora a gente consegue descobrir a profundidade do centro de gravidade
Pelo desenho vemos que será:
Sendo assim, agora conseguimos calcular a força causada pela coluna de liquido.
Agora temos a profundidade e a área do portão é dada na figura no enunciado, temos:
Passo 2
Agora, vamos encontrar o ponto de aplicação, o centro de pressão.
A formula para isso é:
O ângulo que a placa faz com a horizontal é , além disso podemos cortar a densidade mássica, ficando com:
O momento de inércia de uma chapa retangular é:
Substituindo os valores que temos, chegamos em:
Lembrando que esse valor é relação ao centro de gravidade, então temos isso:
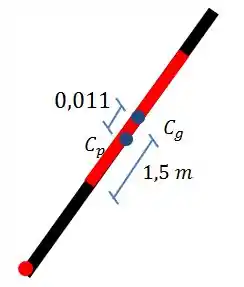
Resposta
Exercício Resolvido #9
A comporta na Figura abaixo é uma massa homogênea de , de largura, é articulada em e está apoiada sobre um fundo liso em . Todos os fluidos estão a . Para qual profundidade da água a força no ponto será zero?
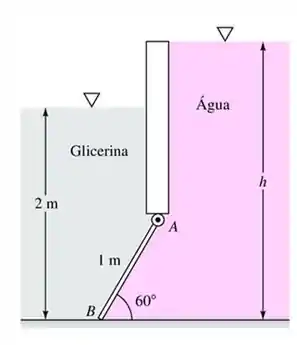
Passo 1
Essa é a questão que mistura tudo que aprendemos, pois temos a comporta exposta a dois fluidos. A comporta está inclinada.
Sabemos que para calcular a força de pressão precisamos saber a posição do centro de gravidade. Então iremos achar a posição do centro de gravidade.
Como a comporta é um retângulo, o centro de gravidade está no meio dela, assim temos:
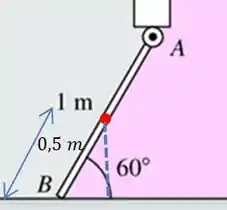
Vamos usar a relação do seno:
Agora a gente consegue calcular a profundidade do centro de gravidade.
Começando pelo lado esquerdo, o lado da glicerina:
A profundidade do centro de gravidade é:
Já no lado da água, teremos uma função, já que não sabemos o valor da coluna de água, na verdade é isso que queremos descobrir, assim:
Passo 2
Sabendo a profundidade do centro de gravidade para cada lado. E também, sabendo que a densidade da água é e da glicerina é . Conseguimos calcular a força de pressão aplicada na placa devido a cada fluido.
Já a força devido a coluna de água será uma função, tendo como variável.
Passo 3
Já encontramos as forças, agora só falta encontrar o ponto de aplicação de cada uma delas.
Começando pela força devido a glicerina, temos:
O momento de inércia da comporta retangular é:
Como o enunciado informou que a largura b é 1,2 m e pela figura temos que o comprimento L da comporta é de 1 m:
Observe que a parte que importa qual fluido se trata se cancela, sendo assim a única coisa que vai mudar de uma equação para a outra será a profundidade do centro de gravidade.
Mas vamos terminar de calcular essa posição antes de tudo:
Agora, vamos calcular a posição para a força devido a água. Usando o que já encontramos:
Passo 4
Show, temos as forças e pontos de aplicação calculados.
Sempre lembrando que esses ponto de aplicação foram calculados em relação ao centro de gravidade, no plano da placa. Não se esqueçam disso, por favor!
Então o que a gente tem é isso:
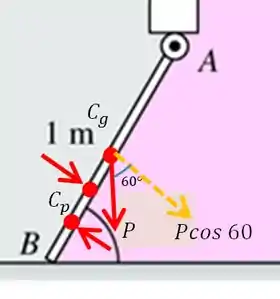
Para podermos aplicar a equação de momento, devemos decompor o peso, pois no momento irá interessar apenas a componente normal a comporta, sendo esta:
Bem, agora podemos aplicar a equação de momento, fazendo o momento em relação ao ponto .
Preste atenção que é no ponto , sendo assim a distância do centro de gravidade a este ponto é .
A distância do centro de pressão da glicerina será a posição do centro de gravidade em relação ao ponto menos a sua posição em relação ao centro de gravidade:
E o mesmo acontecerá com o centro de pressão da água:
Agora sim, aplicando a equação de momento:
Resposta
Exercício Resolvido #10
Na figura abaixo, determinar a altura e a mínima força para que a comporta permaneça em equilíbrio. A largura é unitária. Adotar e
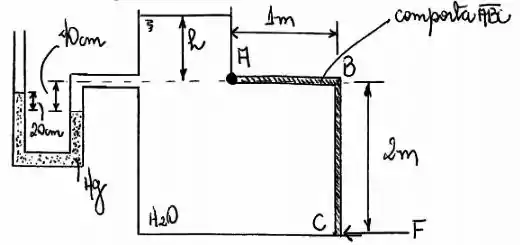
Passo 1
Vamos começar descobrindo o valor de . Para isso vamos usar o princípio de Stevin, ou seja, pegar dois pontos no mesmo fluido na mesma altura e igualar as pressões.
Porém nesse caso dois pontos não será o suficiente para gente resolver o problema, iremos precisar de 4 pontos, os seguintes 4 pontos:
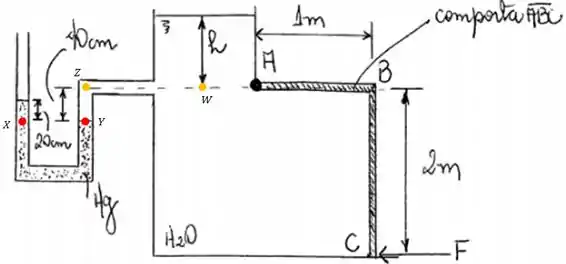
Temos que e
Beleza, vamos então primeiro montar a igualdade de pressão dos pontos laranjas.
A pressão em é devido a pressão atmosférica e a pressão de coluna de água , sendo assim vale:
Agora vamos montar a equação de pressão dos pontos em vermelho.
A pressão em é:
Já a pressão em é:
Igualando as pressões temos:
A pressão atmosférica vai se cancelar, assim sobrando apenas como variável.
Agora que sabemos a altura conseguimos saber a pressão nos pontos e .
Porque a pressão nesse ponto é importante? Pois ela ira exercer uma força na comporta, nessa região.
Como temos a ação da pressão atmosférica na região externa, vamos subtraí-la da conta, assim podemos falar que a pressão em e é:
Como temos a ação de uma pressão constante na superfície da comporta o ponto de aplicação será no centroide da superfície , sendo assim . E podemos calcular a força resultante dessa pressão usando:
A largura, foi dita unitária, 1.
Sendo assim a força aplicada na região é
Passo 2
Agora vamos descobrir a força causada na superfície da comporta. Aqui é onde acontece o que temos estudado e feito vários exercícios.
Assim, a força será dada por:
O centro de gravidade dessa superfície está localizado a do ponto , certo? Metade da chapa.
Sendo assim a profundidade do centro de gravidade é:
Tendo a profundidade do centro de gravidade conseguimos calcular a força.
Agora, só falta encontrarmos a posição em que atua essa força, ou seja, o centro de pressão:
O ângulo que a chapa faz com a superfície é , o momento de inércia de uma chapa é:
Substituindo isso temos:
Como essa posição é em relação ao centro de gravidade, então em relação ao ponto a distância seria:
E a força aplicada no ponto está a do ponto . Bem, para que precisamos saber disso? Para quando aplicarmos a equação de momento sabermos todas as distâncias.
Passo 3
Então agora vamos aplicar a equação de momento, se queremos que a peça esteja parada então,