Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 121
Repita o problema 3-120 para uma altura de água total de .
Passo 1
Temos uma comporta articulada e temos que determinar a força hidrostática que está ocorrendo nele e a distância do centro de pressão da superfície da água. Para ficar melhor ilustrado eu fiz um desenho humilde aqui:
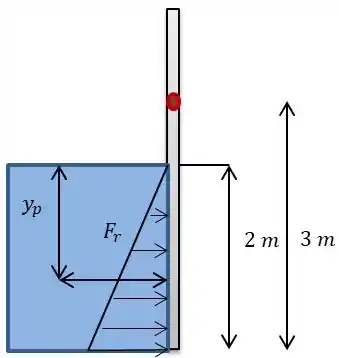
Temos que determinar e .
Assumindo que a pressão atmosférica ocorre nos dois lados da comporta, e por causa disto por convenção podemos desconsidera-la de nossos cálculos.
Tomaremos a densidade padrão da água, .
Passo 2
Podemos determinara a força resultante no centro do portão pela pressão e a área. Como pressão é e força basta multiplicarmos pela área e teremos a força.
Em que é a altura da coluna de água:
Passo 3
A distância vertical do centro de pressão da superfície da água é:
Resposta
Exercícios de Livros Relacionados
A comporta circular ABC na figura abaixo tem um raio de 1 m e é articulada em B. Calcule a força P exatamente suficiente para impedir que a comporta se abra quando h = 8 m. Despreze a pressão atmosfér
Na figura abaixo a comporta AB tem 3 m e largura e está conectada por um cabo e polia a uma esfera de concreto (d = 2,4). Qual é o menor diâmetro da esfera suficiente para manter a comporta fechada?
A comporta AB da figura abaixo é articulada em A, tem a largura b e estabelece um contato suave em B. A comporta tem massa específica ρ s e espessura uniforme t. Para qual massa específica ρ s da comp
A comporta ABC na figura abaixo tem 1 m de quadrado e está articulada em B. Ela abrirá automaticamente quando o nível de h da água se tornar suficientemente alto. Determine a menor altura para a qual
O painel BC na figura a seguir é circular. Calcule (a) a força hidrostática sobre o painel, (b) Seu centro de pressão e (c) o momento dessa força em relação ao ponto B.