Fluido sendo acelerado
Produzido por Raphael EloiTeoria
O que acontece quando se acelera um fluido?
Já tentou correr com um copo de água na mão? Ou já parou para pensar como o fluido vai se comportar em uma situação em que ele está acelerado?
Parece que o fluido anda para trás né? Ele vai sair de uma posição paralela ao chão para uma posição inclinada. Tipo assim:
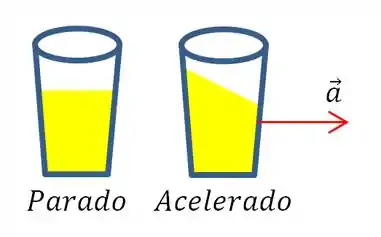
Aqui a gente vai usar a convenção de que o fluido todo está acelerado com a mesma aceleração que o recipiente em que ele está, ok?
O que acontece com o fluido nessas condições é que a distribuição de pressão muda quando ele está acelerado, porque agora vamos precisar levar em conta outros fatores… Vem comigo que vamos ver isso com calma!
Bom, agora não temos mais um comportamento hidrostático. Assim aqueles princípios que estudamos até aqui vão mudar um pouco. A pressão vai variar ao longo da profundidade, como a gente estava acostumado, mas agora temos um novidade na equação! Dá uma olhadinha aqui, a pressão, para um fluido acelerado, será calculada como sendo:
G
Nessa equação temos o que é a densidade do fluido, o que é a profundidade do ponto analisado, que é nossa pressão atmosférica e temos o G! Opa! Quem é esse cara que está em negrito na equação?
Relaxa! É que a gente estava acostumado com o (minúsculo) que indica a aceleração da gravidade, mas nas condições de fluido acelerado a gente vai usar a aceleração efetiva, que é esse maiúsculo aí! É exatamente ele que vai influenciar na pressão.
E como se calcula o G?
Pra gente calcular a aceleração efetiva, vamos usar essa equação aqui, olha só:
Vamo dar uma olhadinha em cada termo dessa equação, ok? Esse é a componente da aceleração, esse é componente da aceleração e o é a nossa velha conhecida, a gravidade.
O representa o módulo da aceleração resultante, ok? Por isso que a gente trabalha com as componentes para encontrar ele! :)
Vamos ficar atento em uma coisa importante, ok? O sinal! Porque agora podemos ter uma questão onde o fluido é acelerado para baixo e em outra questão ele pode ser acelerado para cima… Sendo assim vamos fazer um combinado! Para que continue sendo positivo, vamos usar que é positivo para baixo na direção e positivo para esquerda na direção .
Beleza! Agora que já sabemos como encontrar a pressão e o módulo da aceleração resultante, vamos voltar a observar o nosso fluido no copo, beleza?
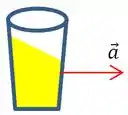
Consegue observar que ele faz uma inclinação? Ele forma um ângulo, bem ali, olha só:
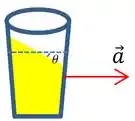
Esse ângulo formado na superfície do líquido com a horizontal pode ser calculado usando essa equação aqui:
Mais uma vez a gente usa o que é a componente da aceleração, o que é a componente da aceleração e o que é a gravidade, beleza?
Diferença de pressão
Lembra que lá no começo a gente falou que em um fluido sendo acelerado, teríamos alteração na pressão e na distribuição da pressão?
É isso aí! E agora vamos ver como vai ficar a nossa diferença de pressão, em um fluido que está sendo acelerado. Ela será dada por:
e a gente já tá ligado que são as componentes da aceleração, certo?
Mas e e ? Bom, vamos lembrar que a diferença de pressão quer dizer que estamos comparando dois pontos, né? Um ponto 1, onde temos o , e o ponto 2, onde temos o . Então esse e são exatamente as distâncias entre os pontos, no eixo e no eixo , belezinha?
Vamos de exemplo?
Um exemplo pra ajudar a gente a entender melhor é sempre bem vindo, não é mesmo?
Estamos de mudança e precisamos transportar um aquário de 50 cm de altura, 2 metros de comprimento e 0,3 metros de profundidade. Ele está cheio até a metade com água. Durante o transporte, variamos a velocidade de 0 a 10 m/s em 5 segundos. Determine o ângulo que a superfície livre faz com a horizontal e calcule a gravidade efetiva nessas condições.
Olha só! Vamos precisar calcular a gravidade efetiva, , e o ângulo, , ok?
Vamos começar encontrando o ângulo, para isso vamos usar a equação que vimos ali em cima:
Mas quem será o e o ? Bom, se estamos transportando um aquário em um linha reta, vamos começar supondo que não existirá uma componente de aceleração em , ok? E a componente em , será dada por:
Substituindo nossos dados temos:
E sabendo que a gravidade é , nosso ângulo será:
Show! E agora precisamos da gravidade efetiva, vamos encontrar ela:
Prontinho! Ficou mais tranquilo de visualizar o que aprendemos agora, né?
E se o fluido estiver inclinado?
Aqui vale uma observação! Quando tivermos o fluido em um plano inclinado, deve ser a distância entre o ponto e a superfície do líquido sem a inclinação, ou seja, você tem que usar apenas a componente dessa distância. Isso é importante para quando tivermos recipientes em um plano inclinado. Olhe a diferença:
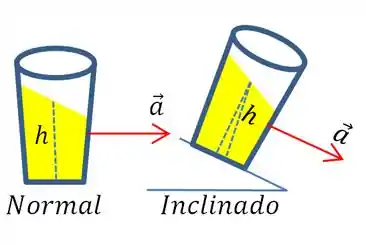
Show de bola! Agora bora para os exercícios!