Difusividade em Gases
Produzido por Raphael EloiTeoria
A gente viu lá na Lei de Fick que o fluxo de difusão é proporcional à a variação de concentração!
Mas proporcional quanto? Essa constante de proporcionalidade entre o quando a matéria se difunde em um meio e a diferença de concentração de um ponto a outro é justamente a difusividade.
Dando uma olhadinha nas dimensões de cada coisa que a gente tem nessa fórmula, a gente descobre que a unidade da difusividade é , no SI . Show?
Mas então, só pra gente ter uma ideia de qual tamanho dessa proporção, vamos dar uma olhadinha aqui nas ordens de grandeza!

A difusividade é uma propriedade de cada molécula se espalhar em um meio específico, e ela vai ser função de algumas condições tipo pressão, temperatura e da própria massa molar desse meio. Bora ver melhor isso ai!
Fatores que influenciam a Difusividade
Analisando as dimensões da difusividade:
Quando a gente “abre” as dimensões da difusividade assim, a gente consegue ver mais claramente que dentro dela tem uma unidade de comprimento e uma velocidade (comprimento sobre tempo). Ai, o que a gente precisa pensar agora é o que é cada coisa. A difusividade é o quanto uma molécula consegue se espalhar em um meio, certo? Então essa unidade de comprimento ai representa o Percurso Livre Médio, que é o quanto de caminho tá livre pra essa molécula se movimentar sem se chocar com outra. A velocidade seria a velocidade média com a qual as moléculas se movem. Isso explica bastante o proque da difusividade dos gases serem bem maiores do que a dos líquidos e dos sólidos. Na fase gasosa as moléculas estão muito mais espalhadas e se movem muito mais energicamente, beleza? Isso que eu acabei de falar não vai ser tãããão importante pra gente em termos práticos porque é tudo microscópio, mas serve pra gente entender um pouquinho a lógica da difusividade.

Caaalma, vai fazer sentido! Vamos olhar agora pras condições macroscópicas e ver como elas influenciam a difusividade:
- Temperatura – Quando maior a temperatura ↑, maior a difusividade ↑. Dando mais energia pras moléculas você aumenta a velocidade delas e elas se difundem mais facilmente.
- Pressão – Quando maior a pressão ↑, menor a difusividade ↓. Aumentando a pressão, mais comprimidas ficam as moléculas e menos é o percurso livre médio.
- Massa molar – Quando maior a massa molar ↑, menor é a difusividade ↓. Quando maior o tamanho da molécula, mais difícil fica de ela passar entre as outras.
Vamos ver então como é que a gente finalmente chega no coeficiente de difusão de cada molécula!
Cálculo do coeficiente de Difusão
Lá beeem antigamente (brincadeira, alguns não tão antigamente assim), uma galera muito gênia modelou varias maneiras de se chegar ao coeficiente de difusão ou a difusividade de moléculas. As demonstrações são bem longas, mas hoje existem alguns modelinhos bem aceitos e eu vou mostrar eles pra você!
- Autodifusão : Esse a gente usa quando estivermos falando da difusão de átomos da mesma espécie ou muito parecidos, como isótopos por exemplo.
- Equação de Hirschfelder, Bird e Spotz: Usada para gases não polares e moléculas não reativas.
- Correlação de Fuller, Schettle e Giddings: é uma correlação empírica e boa pra ser usada quando os parâmetros e não estão disponíveis.
- Método de Brokaw: usado para compostos polares.
Onde d é o diâmetro das moléculas, P é a pressão em atm, m é a massa de uma molécula, k é a constante de Boltzmann () e T é a temperatura em Kelvin.
Onde: é o coeficiente de difusão do soluto A no meio B, e são as massas molares dos componentes A e B respectivamente, T é a temperatura em Kelvin, P é a pressão em atm, é o diâmetro de colisão em Angstroms e é a integral de colisão.
A integral de colisão é medida em ergs e definida como uma função da temperatura e da energia da interação molecular para um sistema binário, ou seja, o quão provável e eficiente são essas colisões. Mas, você pode ficar tranquilo que esses dados são tabelados e você não vai precisar fazer muitas contas pra achar eles!

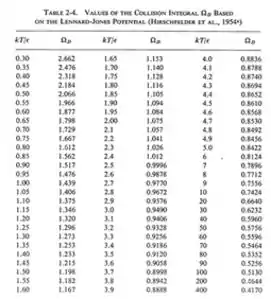
Aqui tem alguns exemplos pra vocês usarem nos exercícios! Essas tabelinhas ai foram tiradas do Hines
Como a difusividade é função da temperatura e pressão, muitas vezes é preciso converter de uma condição para a outra. A correlação que se usa é essa aqui, pro modelo daqui de cima:
Onde é a massa molar e é o volume atômico.
Nesse método você usa a Equação de Hirschfelder, mas o jeito de calcular a integral de colisão é outro, já que é outro tipo de interação molecular:
Onde,
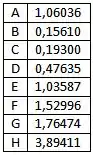
é o componente y da distância entra as colisões moleculares.
Para sendo o momento dipolo, o volume molar no ponto de ebulição e a temperatura no ponto de ebulição.
Por último, repara que por essas relaçõesque a gente viu , justamente porque as moléculas não tem tanta interação entre si, então uma em relação à outra não é relevante pra difusividade. Mas isso só vale pra gases, beleza?
É meio doido, mas vai entrando no sangue conforme a gente faz exercício hehe
Bora exercitar pra ficar mais fácil!
Fatores que influenciam a Difusividade
Cálculo do coeficiente de Difusão
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
A difusividade, propriedade que indica a capacidade de uma substância se difundir em outra, é influenciada por alguns fatores indicados abaixo. Explique como eles influenciam a difusividade!
a) Temperatura
b) Polaridade
c) Pressão
d) Massa molar
Passo 1
Bom, vamos começar analisando a letra a!
Temperatura – Quanto maior a temperatura, mais energia as moléculas vão ter e também maior velocidade de deslocamento uma pelas outras. Logo, quanto maior a temperatura, maior também a difusividade.
Passo 2
Vamos agora ver a letra b!
Polaridade – A polaridade das moléculas influencia a forma como uma substância interagem com a outra, portanto, essa também é uma propriedade que está relacionada com a difusividade. A polaridade das moléculas nos dá uma dica para saber qual é a melhor correlação a ser usada para calcular a difusividade da mistura com maior precisão.
Passo 3
Letra c!
Pressão – Quando falamos de pressão em gases, estamos querendo dizer o quão comprimidas estão as moléculas desse gás. Logo, se a pressão está alta, as moléculas estão bastante comprimidas e com isso, elas tem menos espaço para se deslocarem umas entra as outras. Sendo assim, quanto maior a pressão, menor a difusividade.
Passo 4
Por fim, letra d!
Massa molar – Quanto maior a massa molar, maior é a nossa molécula. E, quanto maior a molécula, mais espaço ela precisa pra sair se deslocando por ai, então fica mais difícil dela passar. Sendo assim, quanto maior a massa molar, menor a difusividade!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração Própria
Demonstre que para gases.
Passo 1
Bom, vamos lá! Para demonstrar que , vamos começar analisando as expressões que usamos para calcular cada um deles.
Começando pela equação de Hirschfelder, Bird e Spotz:
que é o diâmetro de colisão é definido por . que é a integral de colisão, é definida como função da energia de interação molecular e da temperatura.
Repara, que se eu tiver uma mistura de e , não importa quem eu chame de A ou de B, vai ser o mesmo.
Passo 2
Agora, vamos analisar a correlação de Fuller, Schettle e Giddings.
Pra essa correlação, também não importa quem chamamos de A e quem chamamos de B.
Passo 3
Agora vamos fazer uma análise mais profunda. Isso acontece porque em gases, as moléculas estão tão espalhadas e agitadas que não faz diferença quem está em maior ou menor quantidade. Em geral as misturar são muito melhores. Em líquidos, por exemplo, já não podemos considerar a mesma coisa uma vez que o solvente (que está em maior quantidade) envolve o soluto (que está em menor quantidade) e nesse caso faz diferença pra difusão qual molécula está por fora e por dentro, beleza?
Resposta
para gases, como queríamos demonstrar
Exercício Resolvido #3
Welty, J. R., Wicks, C. E., Wilson, R. E., Rorrer, G. L. (2008), Fundamentals of Momentum, Heat and Mass Transfer, 5th edition, John Wiley & Sons, New Jersey, chapter 24, 24.8 (Adaptado)
Determine o valor da difusividade na fase gasosa da mistura de etanol e ar a e usando a correlação de Fuller, Schettle e Giddings.
Passo 1
Pra começar, vamos começar escrevendo aqui então a correlação que a gente vai usar:
Antes de começar sair fazendo conta, a gente tem que verificar se os dados que a gente tem estão nas unidades corretas. Quando a gente dá essa conferida vamos perceber que temos que passar a pressão pra . Sendo assim, nossa pressão vai ser .
Outra coisa é que a gente tem que descobrir quem são a massa molar do Ar e do Etanol e seus respectivos volumes atômicos. Esse valor normalmente são tabelados e é possível achar eles nos livros de transferência de massa.
Passo 2
Os volumes atômicos a gente acha tabelado, e eles são:
As massa molares a gente é capaz de calcular:
Passo 3
Pronto, agora que temos todos os dados que precisamos, é só substituir na fórmula e calcular!
Resposta
Exercício Resolvido #4
Elaboração Própria
Água é purificada através de uma peneira molecular de 3 angstrons na forma de vapor pressurizado à . Calcule o coeficiente de autodifusão da água nessa temperatura.
Passo 1
Pra começar, vamos enunciar a relação que usaremos:
A pressão de vapor da água à é , que é equivalente a .
O diâmetro molecular da água é .
Passo 2
Agora só precisamos substituir os valores e calcular!
Resposta
Exercício Resolvido #5
Welty, J. R., Wicks, C. E., Wilson, R. E., Rorrer, G. L. (2008), Fundamentals of Momentum, Heat and Mass Transfer, 5th edition, John Wiley & Sons, New Jersey, chapter 24, 24.8 (Adaptado)
Determine o valor da difusividade na fase gasosa da mistura de etanol e ar a e usando a equação de Hirschfelder, Bird e Spotz.
Passo 1
Pra começar, vamos começar escrevendo aqui então a correlação que a gente vai usar:
Antes de começar sair fazendo conta, a gente tem que verificar se os dados que a gente tem estão nas unidades corretas. Quando a gente dá essa conferida vamos perceber que temos que passar a pressão pra . Sendo assim, nossa pressão vai ser .
Outra coisa é que a gente tem que descobrir quem são a massa molar do Ar e do Etanol, quem é e quem é .
Passo 2
As massa molares a gente é capaz de calcular:
Agora, para calcular , precisamos encontrar primeiro quem é e .
Como ,
Através da razão a gente acha . Isso ai tá tudo tabelado!
Passo 3
Pronto, agora que temos todos os dados que precisamos, é só substituir na fórmula e calcular!
Resposta
Exercício Resolvido #6
Elaboração Própria
O coeficiente de difusão do dióxido de carbono em ar à e pressão atmosférica é . Qual seria o valor do coeficiente caso estivéssemos avaliando à de temperatura?
Passo 1
Pra começar, vamos começar escrevendo aqui então a correlação que a gente vai usar:
Como a pressão não muda, podemos reescrever dessa forma:
Passo 2
Precisamos então calcular o valor das integrais de colisão nas duas temperaturas.
Para isso vamos calcular antes
Para
Para
Passo 3
Pronto, agora que temos todos os dados que precisamos, é só substituir na fórmula e calcular!
Resposta
Exercício Resolvido #7
Welty, J. R., Wicks, C. E., Wilson, R. E., Rorrer, G. L. (2008), Fundamentals of Momentum, Heat and Mass Transfer, 5th edition, John Wiley & Sons, New Jersey, chapter 24, 24.11
Um torre de absorção é proposta para remover seletivamente amônia de uma corrente de exaustão de gás. Estime a difusividade da amônia no ar à e usando a equação de Brokaw. O momento de dipolo da amônia é .
Passo 1
Pra começar, para usar a relação de Brokaw, a gente calcula o coeficiente de difusão usando a equação de Hirschfelder:
Porém a diferença é que para calcular a integral de colisão, usamos a segunte fórmula:
Onde
Passo 2
Vamos então calcular o !
Agora podemos calcular :
Passo 3
Agora temos que converter esse em :
Pra isso precisamos calcular :
Logo, !
Passo 4
Dos valores tabelados podemos obter
Finalmente podemos calcular a difusividade! (Lembrando que a pressão tem que ser em , viu?)
Resposta
Exercício Resolvido #8
Welty, J. R., Wicks, C. E., Wilson, R. E., Rorrer, G. L. (2008), Fundamentals of Momentum, Heat and Mass Transfer, 5th edition, John Wiley & Sons, New Jersey, chapter 24
Na deposição química de vapor de Silano em uma pastilha de silicone, uma corrente de gás de processo rica em nitrogênio inerte tem a seguinte composição:
A mistura de gás é mantida a 900K e 100Pa. Determine a difusividade do Silano através da mistura de gás. As contantes de Lennard-Joner pro Silano são e .
Passo 1
Pra começar, é preciso calcular os coeficientes de difusão do Silano para cada componente usando equação de Hirschfelder:
Depois precisamos calcular a composição relativa de cada componente na base livre (sem o componente 1):
E por fim, a gente calcula a difusividade na mistura:
Passo 2
Vamos primeiro calcular então a difusividade pra cada componente da mistura pela equação de Hirschfelder:
Passo 3
Agora vamos calcular as composições relativas:
Passo 4
Agora finalmente vamos calcular o coeficiente de difusão da mistura: