Difusividade em Líquidos
Produzido por Raphael EloiTeoria
A difusividade em líquidos é menor do que nos gases. Nos líquidos as moléculas estão mais próximas do que as dos gases, então o caminho livre que essas partículas tem pra se espalhar ai é menor. Além disso, em líquidos a gente tem uma influência muito maior das interações intermoleculares, então além do caminho livre ser menor, as moléculas vão eventualmente se mover mais devagar, beleza?

Bom, falando ainda das interações da molécula com o fluido, imagina que você é um peixe. Se você está nadando contra a corrente, vai ter uma força atuando contra você. Isso sem contar com o atrito que o seu corpo faz com o fluido. A mesma coisa se você estiver nadando a favor da corrente, ainda assim a sua velocidade não vai ser a mesma que a do fluido por causa do seu peso, por causa do atrito. Agora, as duas situações também seriam diferentes se você estivesse nadando no meio de um cardume, certo? Por isso, na difusão de massa em líquidos, a difusividade vai ser diferente pra soluções diluídas e concentradas.
Só uma observação, mas que é importante saber é que essas correlações feitas pra descobrir a difusividade de soluções são encontradas empiricamente, ou seja, através de experimentos que levaram à essas modelagens matemáticas. Então, todas elas possuem um erro associado, ok? Mas pras coisas que a gente precisa descobrir, esse erros são considerados irrelevantes.
Vamos lá falar de cada correlação então, e quando vamos usar cada uma!
Equação de Stokes-Einstein
Você já deve ter falado do regime de Stokes. Se não lembra, basicamente a Lei de Stokes define um fator de fricção no escoamento de uma partícula esférica, em diluição infinita num fluido viscoso em regime laminar. E é baseado nele que Einstein desenvolveu essa expressão pro coeficiente de difusão:
Em que é a constant de Boltzmann (), T é a temperatura em Kelvin, é a viscosidade do fluido e é o raio da partícula.
Essa correlação é usada para partículas coloidais ou moléculas grandes!
Correlação de Wilke e Chang
Usada para não-eletrólitos em diluição infinita.
Onde é a massa molecular do solvente, é o volume molar do soluto (valores tabelados) e é o fator de associação pro solvente.
Correlação para Soluções Concentradas
Quando falamos de soluções concentradas, temos duas correlações possíveis. Uma é simplificada (e menos precisa) e a outra leva em consideração a viscosidade de cada componente da mistura. A gente vai usar sempre a que for mais conveniente com os dados que o problema der pra gente, beleza?
- Correlação de Vignes:
- Correlação de Leffer-Culliman:
Onde , é a fração molar do soluto A e é o coeficiente de atividade do soluto.
Onde é a viscosidade da mistura.
Agora bora exercitar essas correlações :D
Equação de Stokes-Einstein
Correlação de Wilke e Chang
Correlação para Soluções Concentradas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Explique porque a difusividade em líquidos é menor do que em gases.
Passo 1
Quando comparamos a difusão em líquidos e em gases, a gente precisa prestar atenção em algumas coisas.
Em gases, as moléculas estão mais espalhadas, em geral elas são menores e elas só interagem com outras moléculas através de choques.
Em líquidos, as moléculas estão mais próximas, há interação entre o solvente e o soluto (diferença de potencial químico), além disso, existe como se fosse uma força de atrito entre uma molécula e outra quando elas se deslocam. Isso tudo dificulta o deslocamento de uma molécula no meio líquido, fazendo com que a difusividade em líquidos seja bem menor do que a difusividade em gases.
Resposta
Em líquidos, as moléculas estão mais próximas, há interação entre o solvente e o soluto (diferença de potencial químico), além disso, existe como se fosse uma força de atrito entre uma molécula e outra quando elas se deslocam. Isso tudo dificulta o deslocamento de uma molécula no meio líquido, fazendo com que a difusividade em líquidos seja bem menor do que a difusividade em gases.
Exercício Resolvido #2
Elaboração Própria
Qual correlação é mais apropriada para calcular a difusividade nas seguintes situações e porque:
- Células na corrente sanguínea
- Mistura bem diluída de acetona e água
- Xarope de glicose concentrado em água
Passo 1
Vamos analisar a letra a!
Quando falamos de células na corrente sanguínea temos que pensar que células são partículas grandes e que o sangue é um líquido viscoso, logo, a correlação mais apropriada pra esse caso é a Equação de Stokes-Einstein!
Passo 2
Letra b!
Uma mistura de acetona e água é uma mistura não eletrolítica, ou seja, não gera eletrólitos e não conduz corrente elétrica. Como estamos falando de uma mistura diluída, a melhor correlação para ser usada é a de Wilke e Chang!
Passo 3
Agora vamos ver a letra c!
A mistura de glicose e água também é uma mistura não eletrolítica. Mas como nesse caso estamos falando de uma solução concentrada, devemos usar as correlações de Vignes ou de Leffer-Culliman pra corrigir!
Resposta
- Equação de Stokes-Einstein
- Equação de Wilke e Chang
- Correlação de Vignes ou Leffer-Culliman
Exercício Resolvido #3
Elaboração Própria
Demonstre que para líquidos.
Passo 1
Para fazer essa demonstração vamos analisar as correlações que podemos usar para encontrar o coeficiente de difusão em líquidos.
Wilke e Chang:
Repara que para o cálculo, eu preciso de dados do solvente (B) como a massa molecular, o fator de associação e a viscosidade. Já pro soluto (A), eu preciso do volume molar apenas. Sendo assim, faz diferença quem está em maior ou menor quantidade, que é quem eu chamo respectivamente de B e de A.
Passo 2
Vamos olhar também a equação de Stokes-Einstein:
Assim como Wilke e Chang, eu preciso de dados diferente de cada componente da mistura, logo aqui também faz diferença quem é o soluto e quem é o solvente.
Passo 3
Agora fazendo uma análise mais profunda, isso acontece porque em líquidos as moléculas estão bem mais próximas e interagem de forma mais relevante. Então propriedade como a polaridade, o potencial químico, a eletronegatividade, e tudo que diz respeito às interações intermoleculares vai influenciar. Então faz muita diferença nesse caso se você é uma molécula A, cercada de moléculas B, ou se você é uma molécula B cercada de moléculas A.
Resposta
para líquidos, como queríamos demonstrar
Exercício Resolvido #4
Bird, R.B., Stawart, W.E. and Lightfoot, E.N. (2004), Fenômenos de Transporte, 2a ed., LTC, Rio de Janeiro. Capítulo 17.
Estime o valor de de uma solução diluída de TNT (2,4,6-trinitrotolueno) em benzeno a .
Passo 1
Bom, nesse caso ai a gente vai usar a equação de Wilke e Chang, considerando TNT como o componente A e o Benzeno como componente B.
A gente vai precisar correr atrás de alguns dados, que são esses aqui:
Isso aqui tudo é tabelado tá? Dá pra achar nos livros e na internet!
Passo 2
Agora só precisamos substituir tudo na fórmula!
Resposta
Exercício Resolvido #5
Welty, J. R., Wicks, C. E., Wilson, R. E., Rorrer, G. L. (2008), Fundamentals of Momentum, Heat and Mass Transfer, 5th edition, John Wiley & Sons, New Jersey, chapter 24
Estime o coeficiente de difusão do etanol , em uma solução diluída de água a .
Passo 1
Bom, nesse caso ai a gente vai usar a equação de Wilke e Chang, considerando o etanol como o componente A e a água como componente B.
Passo 2
A gente vai precisar correr atrás desses dados que a gente não sabe da fórmula!
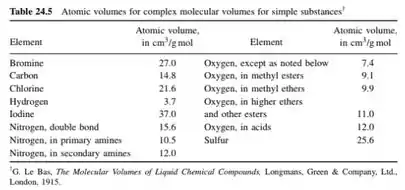
O volume molecular do etanol por exemplo pode ser calculado através dos valores da tabela acima:
A a viscosidade da água é
Passo 3
Agora é só jogar os dados na fórmula e calcular o que queremos!
Resposta
Exercício Resolvido #6
Welty, J. R., Wicks, C. E., Wilson, R. E., Rorrer, G. L. (2008), Fundamentals of Momentum, Heat and Mass Transfer, 5th edition, John Wiley & Sons, New Jersey, chapter 24
Estime a difusividade líquida dos seguintes solutos que são transferidos para soluções diluídas:
- Oxigênio em etanol a 293 K;
- Metanol em água a 283 K.
Passo 1
Bom, todos esses casos a gente vai usar a equação de Wilke e Chang.
Vamos então resolver uma letra de cada vez!
Passo 2
- em etanol a 293K!
- Metanol em água a 283K!
Passo 3
Resposta
Exercício Resolvido #7
Welty, J. R., Wicks, C. E., Wilson, R. E., Rorrer, G. L. (2008), Fundamentals of Momentum, Heat and Mass Transfer, 5th edition, John Wiley & Sons, New Jersey, chapter 24
A equação de Stokes-Einstein é frequentemente usada para estimar o diâmetro molecular de moléculas esféricas grandes através do coeficiente de difusão. A difusividade molecular medida da Seroalbumina (uma importante proteína do sangue) em diluição infinita em água é a 293K. Estime qual valor do diâmetro principal da molécula de Seroalbumina e compare com o valor atualmente conhecido que é 7,22 nm.
Passo 1
Bom, vamos usar então a equação de Stokes-Einstein:
Nos foi dado que , e .
A viscosidade da água nessa temperatura é
Passo 2
Agora vamos jogar esses dados na fórmula para descobrir o diâmetro da partícula!
Resposta
, que é surpreendentemente próximo ao valor conhecido!
Exercício Resolvido #8
Welty, J. R., Wicks, C. E., Wilson, R. E., Rorrer, G. L. (2008), Fundamentals of Momentum, Heat and Mass Transfer, 5th edition, John Wiley & Sons, New Jersey, chapter 24 (Adaptado)
Benzeno (espécie A) é comumente adicionada a etanol para desnaturar o etanol (espécie B). Estime a difusividade em fase líquida do benzeno em etanol e do etanol em benzeno a 293K usando a equação de Wilke-Chang. ?
Passo 1
Bom, vamos usar então a equação de Wilke-Chang:
Fazendo uma de cada vez!
Passo 2
Vamos começar com Benzeno em Etanol.
Passo 3
Agora vamos fazer para Etanol em Benzeno.
Resposta
A difusividade de benzeno em etanol é menor do que a do etanol em benzeno!