Mecanismos de Transferência de Massa
Produzido por Raphael EloiTeoria
Sabe quando a gente bota uma colherinha de açúcar no café e os grãos vão todos pro fundo? Se a gente esperar um tempão é capaz desse açúcar ter dissolvido e o café estar docinho, mas geralmente a gente dá uma mexidinha com uma colher pra acelerar, certo? Então, a gente acabou de descrever 2 mecanismos de transferência de massa: difusão e convecção!

Estes são os principais mecanismos de transferência de massa usados e você vai ver que eles tem muita coisa a ver com o que a gente viu lá na transferência de calor! A difusão é muito parecida com o que a gente chamava de condução e a convecção pra transferência de massa é que nem pra transferência de calor, precisa de um fluido em movimento! Bora lá então ver um poquinho mais sobre eles...
Difusão
Quando entramos naquele metrô lotado, é só a gente ver um espacinho vazio que a gente já quer ir pra lá. Assim como são as pessoas são as moléculas. Elas não gostam de ficar aglomeradas em um canto se elas tiverem um espaço maior pra ficar, e é assim que se dá a difusão molecular. Um experimento legal de se fazer é colocar um M&M em um prato com água, o corante da casquinha vai rapidinho se espalhando pelo prato sem você nem precisar fazer nada! Então vamos lá, a difusão ela acontece pelo movimento aleatórios que as moléculas já tem normalmente, independente de convecção, levando à mistura completa (que é quando todos os pontos do sistema estão à uma mesma concentração).
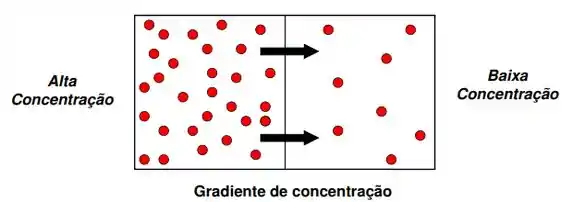
Olhando pra essa figura a gente pode ver que nessa superfície do meio vai ter então um fluxo de transferência de massa! E como a gente equaciona isso? Através da Lei de Fick!
Sendo esse o fluxo molar de difusão e a difusividade de A em B (A é o soluto e B é o solvente). Repara que a Lei de Fick é bem parecida com a Lei de Fourier que a gente viu lá em transcal! O que ela quer dizer basicamente é, o fluxo de transferência de massa é proporcional à diferença de concentração que a gente tem num espaço. E essa constante de proporcionalidade é justamente a difusividade que uma substância tem em relação à outra. Detalhe que nesse caso a ordem dos fatores altera o produto, não necessariamente é igual a , ok? Ah, e nesse caso ai, a concentração do componente A varia espacialmente somente no eixo x, mas pra fazer uma generalização mais correta a gente teria que considerar todas as direções beleza?
Mas aqui a gente vai ver bem mais pro caso unidimensional, relaxa!
Outra coisa é que esse pode ser escrito como ou , e ai se a concentração global é constante, a nossa Lei de Fick fica assim:
Último, porém não menos importante é que ai em cima a gente representou o nosso fluxo molar. Tá, mas e se eu quisesse reprenstar meu fluxo mássico? Aí fica assim:
Em que é a nossa fração mássica, igual a e ρ é a nossa concentração mássica, show?
Convecção
Bom, vamos voltar no nosso experimento com o M&M azul (escolhi essa cor pq é a minha preferida hahaha). Se ao invés de colocarmos ele em um prato a gente colocasse em um copo. O corante ia se difundir também, talvez um pouco mais devagar por a gente colocar um pouco mais de água que colocaria no prato. Mas e se a gente pegasse uma colherinha e mexesse? A água ia ficar azul beeeem mais rápido. Essa transferência de massa pelo movimento do copo na água é o que a gente chama de convecção! E o melhor de tudo, é que a convecção da transferência de massa é equacionado do mesmo jeito que na transferência de calor!
Onde é o fluxo molar de convecção e o h tem esse m sobrescrito pra indicar que a gente está falando de convecção de massa, beleza? Mas se eu quiser falar em fluxo mássico também posso, só usar a concentração mássica ao invés da concentração molar :D
Efeitos Combinados
Falamos da difusão e da convecção, mas e se a gente tiver os dois acontecendo? Bom, na transferência de massa, geralmente os dois mecanismos tem influência muido grande no fluxo total. Então bora entender melhor como é a contribuição de cada um!
Vamos pensar num peixinho nadando contra a corrente de um rio. Concorda que o quando ele tá se movendo em relação ao que está parado em volta é a velocidade que ele nada menos a velocidade de escoamento do rio? Então, por essa lógica que a gente mede a contribuição da difusão na transferência de massa:
Onde esse é a velocidade média que a gente tá vendo o peixinho (ou a nossa molécula) nadar do lado de fora. A diferença entre essa velocidade e a velocidade de escoamento do fluxo que é a velocidade da difusão. Lembrando também que esse é a concentração molar! Se quisermos calcular a contribuição difusiva mássica ficaria assim:
Agora imagina que esse peixinho ao invés de nada ele se deixa levar pelo Rio. A velocidade dele vai ser exatamente a velocidade do rio. Nesse caso, o fluxo vem da contribuição convectiva e ele vai ter essa cara:
ou
Beleza, agora como é que a gente faz pra relacionar os dois? Vamos pegar o fluxo calculado pela contribuição difusiva e comparar ele com a Lei de Fick:
Rearranjando essa igualdade:
Nas correlações de velocidade a gente viu que a velocidade média molar pode ser escrita dessa forma:
Pra um sistema binário a gente teria isso aqui:
Dai rearranjando esses termos na equação a gente chega nisso:
Como a gente pode representar o fluxo total de uma determinada espécie como:
A gente tem pra um sistema binário que:
Generalizando agora pra um sistema multicomponente, finalmente temos que:
Onde esse é a difusividade de A na mistura, beleza? A gente vai falar um pouco melhor dele daqui pra frente!
Bom, agora passando isso de molar para mássico, nossa equação fica assim:
Basicamente isso quer dizer que o fluxo total de um componente é a soma da contribuição difusiva desse componente, e de uma parte do somatório do fluxo convectivo de todos os componentes que estão na mistura. Essa parte é justamente a fração molar ou mássica desse componente, que é como e fosse o “quanto” esse componente pode ser influenciado pela convecção de tudo que tá ali dentro, sacou? Bora exercitar então que isso ai não é fácil, mas rapidinho você vira craque :D
Convecção
Efeitos Combinados
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Em um bécher com 20 ml de uma solução de etanol(A) a ser diluída é adicionado 80 ml de água(B). Sabendo que o coeficiente de difusão do etanol em água é e o bécher tem 5 cm de altura, calcule a concentração final e o fluxo difusivo molar do etanol.
Passo 1
Bom, pra calcular a concentração final vamos usar aquela famosa relação , e pra calcular o fluxo difusivo temos que lembrar da Lei de Fick, que tem essa cara aqui:
Bora então resolver uma coisa de cada vez, partiu!
Passo 2
A gente tinha 20 ml antes, e foram adicionados 80 ml, então o volume final vai ser 100 ml! Agora já podemos fazer a igualdade:
Passo 3
Agora, pra calcular o fluxo difusivo vamos ter que pensar na geometria do nosso problema. A gente tem um bécher com etanol e nele colocamos água. Assim que a gente terminar de colocar a água, no topo do bécher a concentração de etanol vai ser zero, porque nesse momento ele vai estar todo concentrado no fundo. À partir dai vai começar a transferência de massa graças a esse gradiente de concentração. Vamos então calcular esse fluxo!
Obs.: Esse veio da transformação de L para cm³, para a consistência das unidades! É bom ficar ligado nisso
Resposta
Exercício Resolvido #2
Elaboração Própria
Uma piscina retangular de 40.000 L é desinfetada com uma pastilha de cloro de 100 g fixada em um dos cantos na altura do nível da água. Sabendo que as dimensões da piscina são 4 m x 7,5 m x 1,4 m (largura, comprimento e profundidade) e a difusividade do cloro na água é . Calcule o fluxo difusivo mássico total do cloro.
Passo 1
Bom, pra calcular o fluxo difusivo total temos que lembrar da Lei de Fick multidimensional, que tem essa cara aqui:
A gente vai precisar calcular então essa concentração mássica, e ver direitinho quem são dx, dy e dz! Sem esquecer de conferir as unidades! Bora então resolver uma coisa de cada vez, partiu!
Passo 2
A concentração a gente vai calcular usando a massa da pastilha de cloro sobre o volume da piscina:
Passo 3
Outra coisa que a gente vai fazer pra facilitar a nossa vida vai ser converter a unidade do coeficiente de difusão!
Passo 4
Agora vamos analisar as dimensões do problema:
Podemos considerar como sendo a largura, então .
O comprimento vai ser o nosso , então .
Já o nosso , a gente não pode usar essa altura total porque o problema diz que a pastilha fica no nível da água, então vamos ter que descobrir qual é o nosso pelo volume de água na piscina.
Pronto, agora temos tudo que precisamos pra usar a Lei de Fick e achar o fluxo difusivo!
Passo 5
Colocando nossos dados na Lei de Fick:
Resposta
Exercício Resolvido #3
Enade 2014 – Questão 33
Para determinar a taxa molar total da mistura gasosa binária (A+B) deve-se somar as contribuições da transferência de massa por difusão e da transferência de massa por convecção em relação a um ponto estacionário, como apresentada na equação à seguir:
Sendo o coeficiente difusivo, a concentração total e a fração molar do gás A.
Nesse contexto, avalie as afirmações à seguir.
- Quando há contradifusão, a equação simplifica-se para .
- Considerando apenas a direção z, o fluxo molar de um componente numa dada fronteira pode ser calculado com a integração da equação apresentada no enunciado.
- A segunda lei de Fick é o resultado da simplificação da equação da continuidade mássica, considerando o regime transiente, a velocidade do meio nula, a temperatura e pressçao constantes e a ausência de reação química no meio onde ocorre o fenômeno de transferência de massa por difusão.
É correto o que se afirma em
- I, apenas.
- III, apenas.
- I e II, apenas.
- II e III, apenas.
- I, II e III.
Passo 1
Vamos analisar a afirmação I:
- Quando há contradifusão, a equação simplifica-se para .
- Considerando apenas a direção z, o fluxo molar de um componente numa dada fronteira pode ser calculado com a integração da equação apresentada no enunciado.
- A segunda lei de Fick é o resultado da simplificação da equação da continuidade mássica, considerando o regime transiente, a velocidade do meio nula, a temperatura e pressçao constantes e a ausência de reação química no meio onde ocorre o fenômeno de transferência de massa por difusão.
Essa afirmação seria verdadeira se no caso estivéssemos avaliando uma contradifusão equimolar, ou seja, o numero de moles que se deslocam de cada componente devem ser iguais para que . Assim, seria simplificado para . Como o enunciado não diz nada a respeito, não podemos considerar a afirmativa verdadeira.
Passo 2
Agora vamos analisar a afirmação II:
Bom, avaliando nossa equação
Manipulando os termos, chegaríamos na expressão:
Daqui, teríamos que achar uma relação estequimétrica entre e , para que pudéssemos enfim passar esse da esquerda pra direita. Assim, teríamos de um lado e do outro. Passando aquele pra esquerda, finalmente poderíamos integrar em relação à um z específico e encontrar o fluxo molar. Logo, a afirmação é verdadeira!
Passo 3
Por fim, vamos analisar a afirmação III:
A segunda Lei de Fick tem essa cara aqui:
Ela vem do balanço de massa diferencial, quando consideramos o fluido incompressível (ou seja, temperatura e pressão constantes, já que falamos de uma mistura de gases), sem reação química e sem escoamento. Logo, a afirmação está correta!
Resposta
Letra D.
Exercício Resolvido #4
Lista de Exercícios – Transferência de Massa – Prof. Luiz Fernando – UFRJ – 2018
Uma solução ideal contendo de metanol e de benzeno se move com velocidade molar média de . Caso o fluxo molar de benzeno relativo à velocidade média mássica seja , qual é o fluxo molar total de metanol, , e sua velocidade média mássica?
São dados: Metanol (A), , , e Benzeno (B), , .
Passo 1
Bom primeiro vamos organizar os dados que o problema deu pra gente, e pra isso, vou fazer uma tabelinha:

Beleza, agora vamos nos organizar pra chegar aonde queremos!
O fluxo molar de A é dado pela expressão:
E podemos fazer o mesmo pra B!
Também sabemos que a velocidade molar média de uma solução é descrita dessa forma:
Já deu pra visualizar o que que precisamos encontrar? Vamos encontrar as concentrações, para então encontrarmos a velocidade de A e por fim o fluxo! Bora começar então :D
Passo 2
A gente pode relacionar a concentração molar com a densidade e a massa molar por essa relação:
Como a gente já tem essas duas informações, é só resolver a continha e temos que:
Fazendo a mesma coisa pra B encontramos:
.
Como a concentração total de uma solução é a soma das concentrações de cada componente , temos também que:
Passo 3
Agora que já temos isso tudo, vamos encontrar a velocidade de A! Maaaaas, primeiro a velocidade de B! hehe
Com isso podemos achar a velocidade de A!
Passo 4
Agora que a gente tem a concentração de A e a velocidade de A, finalmente podemos calcular o fluxo!
Resposta
Exercício Resolvido #5
Lista de Exercícios – Transferência de Massa – Prof. Lisiane Veiga Mattos – UFF – 2015
Demostre a seguinte relação para sistemas binários:
Passo 1
Bom, já sabemos pela definição que
Abrindo as duas expressões temos
Somando
Passo 2
Agora vamos manipular a seguinte relação:
Substituindo no que tínhamos encontrado antes:
Como , finalmente temos que
Resposta
para um sistema binário, como queríamos demonstrar
Exercício Resolvido #6
Lista de Exercícios – Transferência de Massa – Prof. Lisiane Veiga Mattos – UFF – 2015
Denominando , demonstre que para uma mistura binária:
Passo 1
Bom, pra esse tipo de questão de demonstração, é bom termos em mãos todas as correlações que podemos usar. Agora é uma boa hora pra dar uma lida de novo nos fundamentos!
Vamos então abrir a expressão que a questão deu pra gente:
Sabemos que , logo
Passo 2
Agora usando as seguintes correlações:
Obtemos:
Abrindo os s:
Abrindo :
Colocando em função da fração mássica:
Passando pra dentro:
Finalmente, substituindo , obtemos a expressão desejada:
Resposta
, para um sistema binário.
Exercício Resolvido #7
Enade 2011 – Questão 25 (Adaptada)
A transferência de massa desempenha papel muito importante em muitos processos industriais, como, por exemplo, a remoção de poluentes de um sistema de descarte por absorção, o stripping de gases de águas residuárias, a difusão de substâncias adsorvidas nos poros de um adsorvente e a extração líquido-líquido, entre outros.O mecanismo de transferência de massa depende da dinâmica do sistema no qual esta ocorre. O entendimento dos mecanismos de transferência de massa é muito importante no projeto, otimização e resolução de problemas envolvendo processos de transferência de massa, como os processos de separação.WELTY, J.R., WICKS, C.E., WILSON, R.E., Fundamentals of Momentum, Heat,and Mass Transfer , 3rd Ed., New York: John Wiley and Sons, 1984.Lembrando dos conceitos de transferência de massa, analise as afirmações apresentadas a seguir.I. A Primeira Lei de Fick afirma que a transferência de partículas de uma região para outra é proporcional ao gradiente de concentração. A constante de proporcionalidade é o coeficiente de difusão e é característico da mistura. A Segunda Lei de Fick refere-se à difusão em estado não estacionário.II. A convecção é o mecanismo de transferência de massa através de um fluido em movimento que ocorre apenas de forma forçada. A velocidade de transferência de massa de um soluto é resultado do movimento convectivo (movimento do fluido) e do movimento difusivo (diferença de concentração).III. A Lei de Fick associa o coeficiente de difusão ao inverso da resistência a ser vencida pelo soluto.É correto apenas o que se afirma em
- I
- III
- I e II
- I e III
- II e III
Passo 1
Bom, vamos analisar primeiro a afirmação I.
- A Primeira Lei de Fick afirma que a transferência de partículas de uma região para outra é proporcional ao gradiente de concentração. A constante de proporcionalidade é o coeficiente de difusão e é característico da mistura. A Segunda Lei de Fick refere-se à difusão em estado não estacionário.
- A convecção é o mecanismo de transferência de massa através de um fluido em movimento que ocorre apenas de forma forçada. A velocidade de transferência de massa de um soluto é resultado do movimento convectivo (movimento do fluido) e do movimento difusivo (diferença de concentração).
- A Lei de Fick associa o coeficiente de difusão ao inverso da resistência a ser vencida pelo soluto.
A gente sabe que a primeira Lei de Fick tem essa cara aqui:
E a segunda Lei de Fick essa cara aqui:
O coeficiente de difusão é característico da mistura de A e B. Logo, a Afirmação está correta!
Passo 2
Agora vamos analisar a afirmação II.
A convecção é um mecanismo que pode acontecer de forma natural e forçada, logo, a afirmação está incorreta!
Passo 3
Finalmente, analisando a afirmação III.
Assim como em TransCal, a resistência de condução era o inverso da condutividade térmica, na transferência de massa também fazemos essa associação. O coeficiente de difusão, ou a difusividade, mede o quão fácil é para uma substância se difundir em um meio, ou seja, isso é o inverso da resistência à difusão. Portanto, a afirmação está correta!
Resposta
Letra D.
Exercício Resolvido #8
Lista de Exercícios – Transferência de Massa – Prof. Lisiane Veiga Mattos – UFF – 2015
A partir de demonstre que:
Passo 1
Bom, vamos começar abrindo nossa expressão:
Usando a definição:
Colocando em termos da fração molar () :
Como podemos dizer que
Passo 2
Como e são constantes, vamos colocar eles pra dentro dos somatórios:
Agora vamos juntar tudo:
Abrindo
Por definição , assim, conseguimos finalmente chegar na expressão:
Resposta
, como queríamos demonstrar