1 - Considere a parede plana da Figura 3.1, que separa dois fluidos, um quente e o outro frio, a temperaturas e , respectivamente. Usando balanços de energia nas superfícies e como condições de contorno (veja a Equação 2.34), obtenha a distribuição de temperaturas no interior da parede e o fluxo térmico em termos de .
Passo 1
Desenhe o diagrama do corpo livre da parede plana,
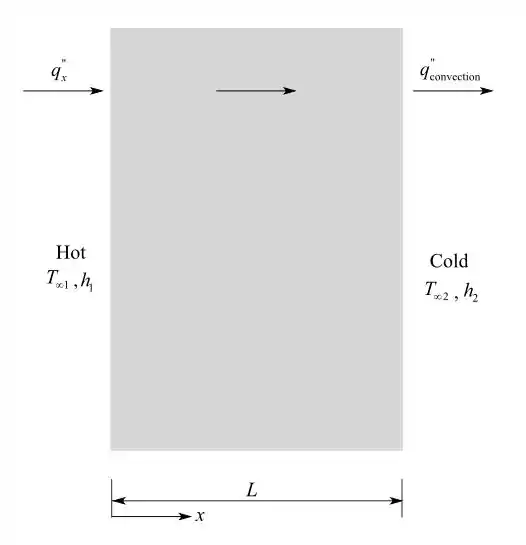
Passo 2
Escreva a equação de condução de calor unidimensional para condições de estado estacionário sem geração interna de calor, como mostrado abaixo:
Aqui, é a condutividade térmica do material e é o gradiente de temperatura ao longo da direção .
Suponha que a condutividade térmica permaneça constante. Assim, a equação acima se torna,
Integre a equação acima,
Novamente, integre a equação acima,
Aqui são constantes de integração.
Passo 3
Encontre as constantes de integração aplicando as condições de contorno.
Primeira condição de contorno:
Em , a convecção da superfície esquerda para o fluido quente é igual à transferência de calor por condução.
Segunda condição de contorno:
Em , a convecção da superfície direita para o fluido frio é igual à transferência de calor por condução
Agora, desde a primeira condição de contorno, reduza uma expressão simplificada,
Aqui é o coeficiente de transferência de calor do fluido quente e é a temperatura do fluido quente.
Encontre o valor da temperatura usando a equação
Substituo por na equação ,
Passo 4
Agora, da segunda condição de contorno, reduza outra expressão simplificada,
Aqui é o coeficiente de transferência de calor do fluido frio e a temperatura do fluido frio.
Passo 5
Para obter a distribuição de temperatura e aquecer fluxo em termos de . As equações e são multiplicadas pelos coeficientes de transferência de calor da seguinte forma:
Multiplique a equação (3) por .
Multiplique a equação por .
Passo 6
Adicione as equações e .
Passo 7
Considere a equação .
Substitua o valor de na equação acima.
Passo 8
Considere a equação (1).
Substitua os valores de e na equação acima.
Portanto, a distribuição de temperatura dentro da parede plana é:
Passo 9
Encontre o fluxo de calor usando a lei de Fourier da taxa de condução de calor,
Substitua por .
Substitua o valor de na relação acima,
Portanto, o fluxo de calor dentro da parede é,
Resposta
A distribuição de temperatura dentro da parede plana é:
O fluxo de calor dentro da parede é: