Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 42
Seja a parede de um tubo com raios interno e externo iguais a e , cujas temperaturas são mantidas a Ti e Te, respectivamente. A condutividade térmica do material do tubo é função da temperatura e pode ser representada por uma expressão na forma k = ke(1 + aT), na qual ke e a são constantes. Obtenha uma expressão para a taxa de transferência de calor por unidade de comprimento do tubo. Qual é a resistência térmica da parede do tubo?
Passo 1
Beleza galerinha, vamos lá! A partir do Eq. 3.29, a forma apropriada da lei de Fourier é:
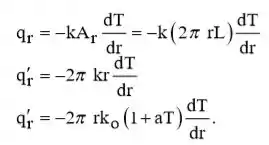
Separação de variáveis,
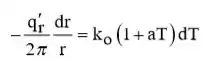
E integrando-se através da parede,
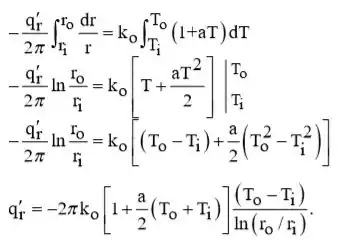
Passo 2
Segue-se que a resistência térmica global por unidade de comprimento é
Resposta
Exercícios de Livros Relacionados
Considere uma parede plana composta constituída por dois materiais com condutividades térmicas k A = 0,09W / ( m · K ) e k B = 0,03W / ( m · K ) e espessuras L A = 8m m e L B = 16m m . A resistência d
Considere um transistor de potência encapsulado em uma caixa de alumínio que é fixado em sua base a uma placa quadrada de alumínio de condutividade térmica k = 240W / m ⋅ K , espessura L = 8m m e larg
Um longo fio de Constantan de 1m m de diâmetro é soldado a topo à superfície de um grande bloco de cobre, formando uma junção de termopar. O fio se comporta como uma aleta, permitindo que o calor flua
Um dissipador de calor de alumínio ( k = 230W / m ⋅ K ), usado para resfriar uma matriz de chips eletrônicos, consiste em um canal quadrado de largura interna w = 30m m , através do qual o fluxo de lí
Considere a água do Exemplo 1.5 como sendo inicialmente líquida em sua temperatura de fusão. A superfície da parede externa é repentinamente reduzida para T 1 = - 30 ° C , resultando na solidificação