Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 85

Considere um forno circular que tem 0,3 m de comprimento e 0,3 m de diâmetro. As duas extremidades têm superfícies cinzas e difusas, que são mantidas a 400 e 500 K, com emissividades de 0,4 e 0,5, respectivamente. A superfície lateral também é cinza e difusa, com uma emissividade de 0,8 e uma temperatura de 800 K. Determine a transferência radiante líquida em cada uma das superfícies.

Passo 1

Vamos lá! Pra começar com o pé direito vamos pegar todas as informações do nosso problema e fazer um esqueminha:

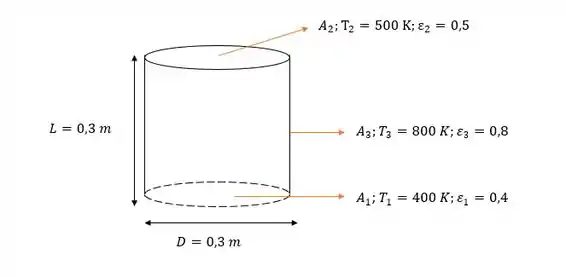
E o que queremos é achar q 1 , q 2   e q 3 !! Para isso vamos fazer:

q i = ∑ j = 1 N J i - J j A i F i j - 1

Lembrando que q i :

q i = E b i - J i 1 - ε i ε i A i

Então primeiro descobrimos J i e depois substituimos para achar q i :

E b i - J i 1 - ε i ε i A i = ∑ j = 1 N J i - J j A i F i j - 1

Podemos cortar as áreas:

E b i - J i 1 - ε i ε i = ∑ j = 1 N J i - J j F i j - 1

Passo 2

Bora montar as equações para cada caso!!!

A 1 :

E b 1 - J 1 1 - ε 1 ε 1 = J 1 - J 2 F 12 - 1 + J 1 - J 3 F 13 - 1

A 2 :

E b 2 - J 2 1 - ε 2 ε 2 = J 2 - J 1 F 21 - 1 + J 2 - J 3 F 23 - 1

A 3 :

E b 3 - J 3 1 - ε 3 ε 3 = J 3 - J 1 F 31 - 1 + J 3 - J 2 F 32 - 1

Precisamos dos fatores de forma!!

Passo 3

As superfícies 1 e 2 são discos paralelos coaxiais, para descobrir F 12 , vamos usar as relações da tabela 13.2 , depois usamos outras relações pra descobrir os outros fatores de forma:

R 1 = R 2 = r L = 0,3 2 0,3 = 0,5

S = 1 + 1 + R 2 2 R 1 2 = 1 + 1 + 0,5 2 0,5 2 = 6

Para calcular F 12 :

F 12 = 1 2 S - S 2 - 4 D 2 D 1 2 1 2

Substituindo:

F 12 = 1 2 6 - 6 2 - 4 0,3 0,3 2 1 2 = 0 , 17

Pela regra da simetria:

F 12 = F 21

Pela regra da soma:

F 13 = 1 - 0 , 17 = 0,83

Pela regra da simetria novamente:

F 13 = F 23 = 0,83

Só falta F 31 e F 32 , que são iguais, pela regra da simetria!

A 3 F 31 = A 1 F 13

Calculando:

F 31 = A 1 A 3 F 13 = π 0,3 2 4 π 0,3 × 0,3   × 0,83 = 0,21

Passo 4

A 1 :

5,67 × 10 - 8 × 400 4 - J 1 1 - 0,4 0,4 = J 1 - J 2 0,17 - 1 + J 1 - J 3 0 , 83 - 1

1451,52 - J 1 = 0,255 J 1 - J 2 + 1,245 J 1 - J 3

2,5 J 1 - 0,255 J 2 - 1,245   J 3 = 1451,52

A 2 :

5,67 × 10 - 8 × 500 4 - J 2 1 - 0,5 0,5 = J 2 - J 1 0,17 - 1 + J 2 - J 3 0,83 - 1

2 J 2 - 0,17 J 1 - 0,83 J 3 = 3544

A 3 :

5,67 × 10 - 8 × 800 4 - J 3 1 - 0,8 0,8 = J 3 - J 1 0,21 - 1 + J 3 - J 2 0,21 - 1

1,105   J 3 - 0,0525 J 1 - 0,0525 J 2 = 23 224,32

Temos 3 equações:

2,5 J 1 + 0,255 J 2 + 1,245   J 3 = 1451,52

2 J 2 - 0,17 J 1 - 0,83 J 3 = 3544

1,105   J 3 - 0,0525 J 1 - 0,0525 J 2 = 23224,32

Podemos achar:

J 1 = 112513   W / m 2  

J 2 = 96417   W / m 2

J 3 = 205016   W / m 2

Passo 5

Podemos finalmente calcular as taxas de calor!!!

q i = E b i - J i 1 - ε i ε i A i

Começando por q 1 :

q 1 = 5,67 × 10 - 8 × 4 00 4 - 112513 1 - 0,4 0,4 × π 0,3 2 4 = - 5233,6   W

q 2 :

q 2 = 5,67 × 10 - 8 × 500 4 - 96417 1 - 0 , 5 0 , 5 × π 0,3 2 4 = - 6564,8   W

q 3 :

q 3 = 5,67 × 10 - 8 × 8 00 4 - 20501 , 6 1 - 0 , 8 0 , 8 × π 0,3 2 = 3080   W

Resposta

q 1 = - 5233,6   W

q 2 = - 6564,8   W

q 3 = 3080   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere os dois discos em forma de anel, coaxiais e paralelos, mostrados na figura.Mostrar que F 12 pode ser representado por, F 1 2 = 1 A 1 { A 1,3 F 1,3 2,4 - A 3 F 3 2,4 - A 4 F 4 1,3 - F 41 } Co
Um cone circular e um cilindro circular com o mesmo diâmetro e comprimento ( A 2 ) estão posicionados coaxialmente, a uma distância L o , de um disco circular ( A 1 ) , como mostrado no esquema. As su
O método dos “filamentos cruzados” de Hottel [7] fornece um meio simples para calcular fatores de forma entre superfícies que têm extensão infinita em uma direção. Para duas destas superfícies (a) com
Considere as seguintes fendas, cada uma com largura W, que foram usinadas em um bloco de material sólido.Para cada caso, obtenha uma expressão para o fator de forma da fenda com relação à vizinhança f
Deduza expressões para o fator de forma F12 associado aos arranjos a seguir. Expresse os seus resultados em termos de A1, A2 e qualquer outra área de superfície hipotética apropriada, assim como do fa