Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 19
A parede de um forno de secagem é construída com a colocação de um material isolante de condutividade térmica k = 0,05 W/ (m · K) entre folhas finas de metal. O ar no interior do forno está a T∞,i = 300°C e o coeficiente convectivo correspondente é hi = 30 W/(m2 · K). A superfície interna da parede absorve um fluxo radiante de q″rad = 100 W/m2 vindo de objetos quentes no interior do forno. A temperatura no ambiente externo do forno é T∞,e = 25°C e o coeficiente total para a convecção e a radiação na superfície externa é he = 10 W/(m2 · K).
(a) Desenhe o circuito térmico para a parede e identifique todas as temperaturas, taxas de transferência de calor e resistências térmicas.
(b) Qual espessura L do isolamento é necessária para manter a superfície externa da parede a uma temperatura segura para o toque de Te = 40°C?
Passo 1
Vamos analisar a questão juntos pra entendermos o que você deve fazer para revolvê-la.
Vamos ver o esquema abaixo:
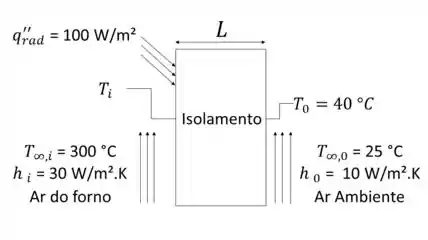
É possível observar na figura que o fluxo de calor radiante é absorvido pela superfície interna fazendo com que a temperatura nesta interface atinja uma temperatura maior que as temperaturas da superfície externa. Além disso, há convecção a partir da temperatura do ar no interior do forno e também na parte exterior com ar ambiente a .
A questão quer que a gente expresse o circuito térmico dessa parede e também que a gente calcule a espessura do isolamento necessária para manter a temperatura da parede externa em 40 °C.
Antes da gente ir pro passo 2, quero que você guarde algumas propriedades que vamos usar:
Passo 2
Para resolver o item (a), basta olharmos o esquema do problema no Passo 1 e a legenda abaixo dela explicando os processos de transferência de calor. Sendo assim, o circuito térmico pode ser expresso pela figura:
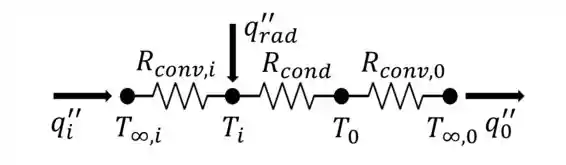
Sendo , e as resistências térmicas convectiva do interior do forno, condutiva e convectiva na superfície externa do forno, respectivamente.
Passo 3
Agora, vamos resolver o item (b):
Para encontrar a espessura L, devemos fazer dois balanços de energia, um no nó e outro no nó .
Fazendo um balanço no nó :
Fazendo um balanço no nó :
Calculando as resistências térmicas pela definição, tem-se que:
Podemos colocar a temperatura em função de L:
Combinando as duas equações e o resultado para :
Resposta
Como demonstrado no Passo 3, .