As janelas de vidro de um automóvel têm área superficial A = 2,6 m2 e espessura t = 4 mm. A temperatura externa é de T∞,e = 32°C, enquanto o compartimento dos passageiros é mantido a T∞,i = 22°C. O coeficiente convectivo na superfície externa dos vidros é igual a he = 90 W/(m2 · K). Determine o ganho de calor pelas janelas quando o coeficiente convectivo interno é de hi = 15 W/(m2 · K). Controlando o escoamento do ar no compartimento dos passageiros, o coeficiente convectivo interno pode ser reduzido para hi = 5 W/(m2 · K), sem sacrificar o conforto dos passageiros. Determine o ganho de calor pelas janelas no caso do coeficiente convectivo interno reduzido.

Vamos analisar a questão juntos pra entendermos o que você deve fazer para revolvê-la.

Temos uma parede composta, onde calor está sendo transferido do ar ambiente para o vidro do carro, por convecção, e, depois, é transferidao entre as paredes do vidro por condução e, por fim, é transferido para dentro do carro por convecção.

A questão quer, então, que a gente encontre a taxa de transferência de calor em duas diferentes situações com dois coeficientes de transferência de calor por convecção.

A gente vai calcular essas taxas seguindo um esquema ilustrativo para o circuito térmico do problema:

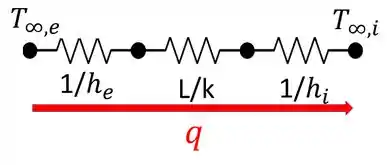
Podemos notar que temos duas resistências à transferência de calor por convecção e uma por condução. Sendo assim, a taxa de calor pode ser expresso como:

Antes de irmos pro Passo 2, quero que você guarde algumas propriedades que vamos utilizar: