Considere o forno do Problema 1.54. As paredes são constituídas por uma camada de isolante, com L = 30 mm de espessura e caracterizado por kiso = 0,03 W/(m · K). O isolante encontra-se entre duas finas camadas de uma folha metálica. A superfície externa do forno está exposta ao ar a 23°C com hext = 2 W/(m2 · K). A temperatura do ar no interior do forno é de 180°C. Desprezando a radiação térmica, determine o fluxo térmico, em regime estacionário, através das paredes do forno, quando a modo convectivo encontra-se desativado e o coeficiente de transferência de calor por convecção natural na superfície interna do forno for de hcn = 3 W/(m2 · K). Determine o fluxo térmico através das paredes do forno, quando a modo convectivo encontra-se ativado e, por sua vez, o coeficiente de transferência de calor por convecção forçada na superfície interna do forno for hcf = 27 W/(m2 · K). A operação do forno no seu modo convectivo resulta em um aumento significativo das perdas térmicas do forno para a cozinha? A sua conclusão mudaria se a radiação fosse incluída em sua análise?
Passo 1
Vamos analisar a questão juntos pra entendermos o que você deve fazer para revolvê-la.
Em primeiro lugar, vamos olhar o esquema abaixo:
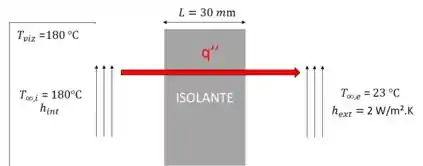
Temos aqui um forno que funciona em dois modos: (1) com convecção natural, com coeficiente de transferência de calor e (2) com convecção forçada, com coeficiente de transferência de calor .
Devemos calcular o fluxo de transferência de calor nos dois modos de funcionamento, expressando o fluxo como uma relação entre a diferença de temperatura do forno e do ar ambiente e a resistência total, por convecção e por condução, ao longo do sistema analisado:
Posteriormente, iremos incluir transferência de calor por radiação em nossa análise. Devemos adicionar uma resistência à transferência de calor por radiação à equação demonstrado acima. Essa resistência pode ser expressa como:
Vou te explicar direitinho como calcular essa resistência mais pra frente, não se preocupe!
Antes de irmos pro Passo 2, quero que você guarde algumas propriedades que vamos utilizar:
Passo 2
Em primeiro lugar, vamos analisar a situação (1) (convecção natural).Nesse caso, . Basta, então, que a gente substitua os dados na equação definida no Passo 1:
Agora, vamos analisar a situação (2) (convecção forçada).Nesse caso, :
Ou seja, com o modo convectivo ligado o forno perde 19,3% a mais de calor para a cozinha.
Passo 3
Agora, vamos analisar as mesmas situações adicionando a resistência à transferência de calor por radiação.
Em primeiro lugar, vamos encontrar uma expressão para calculá-la a partir da equação definida no Passo 1.
Primeiro, a expressão para o fluxo de transferência de calor por radiação é dado por:
Sendo a emissividade do material do interior do forno que, para esse problema, podemos considerar igual a 1, pois o enunciado não nos fornece nenhuma informação; , é a constante de Stefan-Boltzmann e é a temperatura da superfície interior do forno, que não é fornecida, mas podemos aproximá-la como uma média das temperaturas no interior e exterior do forno, sendo assim:
Lembrando que para calcular fluxos por radiação, devemos utilizar a temperatura em . Vamos substituir os valores na equação:
Portanto, a resistência à radiação é:
Agora vamos calcular os fluxos de calor totais com a adição da radiação para cada uma das duas situações analisadas no Passo 2.
Antes disso, se atente para o fato de que a as transferências de calor por radiação e convecção no interior do forno ocorrem simultaneamente. Logo, a resistência equivalente entre eles deve ser calculado como uma resistência em paralelo:
Logo, a equação para o fluxo total se torna:
Calculando o fluxo para a situação (1):
Calculando o fluxo para a situação (2):
Com o modo convectivo ligado, tivemos um aumento de apenas 1,9% na perda de calor. Ou seja, ao considerarmos a radiação, a convecção não é tão importante para o cálculo do fluxo de calor.
Resposta
As respostas estão demonstradas nos Passos 2 e 3.