Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 105

105 - O ar a 15 ° C e 1   a t m flui sobre uma placa de 0,3   m de largura a 65   °   C a uma velocidade de 3,0   m / s . Calcule as seguintes quantidades em  x   =   0,3   m e  x   =   x c r ;

( A ) hidrodinâmica espessura da camada limite, m .

( B ) Coeficiente de atrito local

( C ) Coeficiente médio de atrito

( D ) Tensão de cisalhamento local devido ao atrito, N / m 2

( E ) Força total de arrasto, N

( F ) Espessura da camada limite térmica, m

( G ) coeficiente de transferência de calor por convecção local, W m 2 ⋅ K  

( H ) Coeficiente de convecção médio de transferência de calor, W m 2 ⋅ K

( J ) Taxa de transferência de calor por convecção, W

Passo 1

Dados fornecidos:

Temperatura do fluxo de ar,  T ∞ = 15   ℃

Largura da placa,  w = 0,3   m

Temperatura da placa,  T s = 65   ℃

Velocidade do fluxo de ar  V = 3   m / s

Passo 2

Figura mostrando o fluxo de ar sobre a placa,

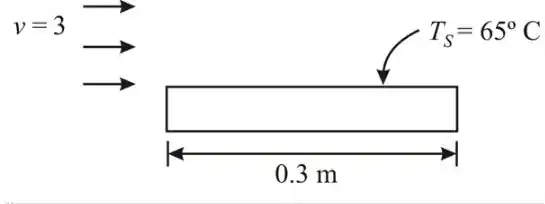
Passo 3

Suposição:

(i) O fluxo é estável e incompressível

(ii) As superfícies da placa são lisas.

Solução: Como também precisamos encontrar as quantidades em  x = x c r .

Vamos calcular o comprimento crítico da placa, isto é,  x c r .

x c r = R e ⋅ μ V ⋅ ρ

Tomando as propriedades do ar na temperatura do filme

T f = T s + T ∞ 2

= 65 + 15 2

T f = 40   ℃  

Passo 4

Com a pressão de 1   a t m e temperatura média do filme 45   ℃ , temos:

O número Prandtl é:

P r = 0,7255

Condutividade térmica é:

k = 0,02662 W m ⋅ ℃

Densidade é:

ρ = 1,127   k g / m 3

Viscosidade dinâmica é:

μ = 1,918 × 10 - 5 k g m ⋅ s

Temos também que o calor específico da água a uma temperatura média de 4 5   ℃ é:

c p = 1007 J k g ⋅ ℃

Passo 5

Vamos rescrever a equação do comprimento crítico da placa para achar R e .

x c r = R e ⋅ μ V ⋅ ρ

R e x = 0,3 = V × x × ρ μ

= 3 × 0,3 × 1,127 1,18 × 10 - 5

R e x = 0,3 = 52883,2

Passo 6

  1. Espessura da camada limite hidrodinâmica.

    2. δ 0,3 = 5 x R e x

    = 5 × 0,3 52883,2

    δ 0,3 = 6,53 × 10 - 3   m

    δ c r = 5 × 2,34 5 × 10 5

    δ c r = 0,020   m

    Passo 7

  2. Coeficiente de atrito local,

    3. C f = 0,664 R e x - 0,5

    = 0,664 52883,2 - 0,5

    C f = 2,887 × 10 - 3

    C f r c r = 0,664 5 × 10 5 - 0,5

    C f r c r = 9,39 × 10 - 4

    Passo 8

  3. Coeficiente de atrito médio.

    4. C f = 1,33 R e x 1 2

    = 1,33 52883,2 1 2

    C f = 5,784 × 10 - 3

    C f c r = 1,33 5 × 10 5 1 2

    C f c r = 1,881 × 10 - 3

    Passo 9

  4. Tensão de cisalhamento local devido ao atrito.

    5. T s = C f ρ V 2 2

    = 5,784 × 10 - 3 × 1,127 × 3 2 2

    T s = 0,02933   N / m 2

    T c r = 1,881 × 10 - 3 × 1,127 × 3 2 2

    T c r = 9,539 × 10 - 3   N / m 2

    Passo 10

  5. Força total de arrasto:

    6. F f = C f A s ρ V 2 2

    = 5,784 × 10 - 3 × 0,3 2 × 1,127 × 3 2 2

    F f = 2,64 × 10 - 3   N

    F c r = 1,881 × 10 - 3 × ( 2,84 × 0,3 ) × 1,127 × 3 2 2

    F c r = 8,125 × 10 - 3   N

    Passo 11

  6. Espessura da camada limite térmica

    7. δ t = 5 x P r 1 3 R e x

    = 5 × 0,3 0,7255 1 3 52883

    δ t = 7,259 × 10 - 3   m

    δ t c r = 5 × 2,84 0,7255 1 3 5 × 10 5

    δ t c r = 0,0223   m

    Passo 12

  7. Coeficiente local de transferência de calor;  h

    8. h x = k x ⋅ N u

    Portanto,

    N u = 0,332 R e x 1 / 2 P r 1 / 3

    = 0,332 × 52883,2 1 2 0,7255 1 / 3

    N u = 68,6

    h x = 68,6 × 0,02662 0,3

    h x = 6,087 W m 2 ⋅ ℃

    Agora, N u c r = 0,332 × 5 × 10 5 0,5 0,7255 1 / 3

    N u c r = 210,95

    h c r = 210,95 × 0,02662 2,84

    h c r = 1,977   W m 2 ⋅ ℃

    Passo 13

  8. Coeficiente médio de transferência de calor, h m e d .

    9. N u x = 0,664 R e x 1 / 2 P r 1 / 3

    = 0,664 × 52883,2 1 2 0,7255 1 / 3

    N u x = 137,2

    h x = k x ⋅ N u x

    h x = 137,2 × 0,02662 0,3

    h x = 12,17   W m 2 ⋅ ℃

    Agora, N u c r = 0,664 × 5 × 10 5 0,5 0,7255 1 / 3

    N u c r = 421,89

    h c r = 421,89 × 0,02662 2,84

    h c r = 3,95   W m 2 ⋅ ℃

    Passo 14

  9. Taxa de transferência de calor

Q x = h A s ( T s - T ∞ )

= 12,17 × ( 0,3 × 0,3 ) ( 65 - 15 )

Q x = 54,765   W

Q c r = h c r ⋅ A S ( T s - T ∞ )

= 3,95 × 2,84 × 0,3 × ( 65 - 15 )

Q c r = 168,27   W

Resposta

a) δ 0,3 = 6,53 × 10 - 3   m

δ c r = 0,020   m

b) C f = 2,887 × 10 - 3

C f r c r = 9,39 × 10 - 4

c) C f = 5,784 × 10 - 3

C f c r = 1,881 × 10 - 3

d) T s = 0,02933   N / m 2

T c r = 9,539 × 10 - 3   N / m 2

e) F f = 2,64 × 10 - 3   N

F c r = 8,125 × 10 - 3   N

f) δ t = 7,259 × 10 - 3   m

δ t c r = 0,0223   m

g) h x = 6,087 W m 2 ⋅ ℃

h c r = 1,977   W m 2 ⋅ ℃

h) h x = 12,17   W m 2 ⋅ ℃

h c r = 3,95   W m 2 ⋅ ℃

i) Q x = 54,765   W

Q c r = 168,27   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mercúrio líquido a 250°C está escoando em paralelo ao longo de uma placa plana na velocidade de 0,3 m/s. A temperatura de superfície da placa de 0,1 m de comprimento é constante a 50°C. Deterime (a) o
Considere um caminhão de refrigeração viajando a 110 km/h em um localonde a temperatura do ar é de 25°C. O comportimento frigorífico do caminhão pode ser considerado como uma caixa retangular de 2,8 m
O óleo de um motor quente a 150°C está fluindo em paralelo ao longo da placa plana a velocidade de 2 m/s. A temperatura da superfície de uma placa plana de 0,5 m de comprimento é constante a 50ºC. Det
O peso de uma placa plana fina de 50 cm x 50 cm de tamanho é equilibrado por um contrapeso de uma massa de 2 kg, conforme mostrado abaixo. Agora um ventilador é ligado, e o ar a 1 atm e 25°C escoa par
Mercúrio líquido a 250°C está escoando na velocidade de 0,3 m/s em paralelo ao longo de uma placa plana de 0,1 m de comprimento, onde há um comprimento inicial sem aquecimento de 5 cm. A seção aquecid