Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 22

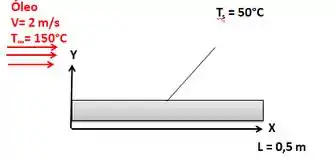
O óleo de um motor quente a 150°C está fluindo em paralelo ao longo da placa plana a velocidade de 2 m/s. A temperatura da superfície de uma placa plana de 0,5 m de comprimento é constante a 50ºC. Determine (a) o coeficiente local de transferência de calor por convecção em 0,2 m a partir do bordo de ataque e o coeficiente médio de transferência de calor de convecção, e (b) repita a parte (a) usando a correlação do Churchill e Ozoe (1973).

Passo 1

(a) Como sempre, precisamos primeiro calcular o valor de reynold para entendermos como é o comportamento do fluido na posição desejada, que nesse caso é em X = 0,5 m

Vamos pegar as propriedades do óleo na temperatura de filme e depois calcular reynold, belê?

T f = 150 + 50 2 = 100 ° C

K = 0,14 W m . K

v = 2,05   x   10 - 5 m 2 s

P r = 279

R e x = V X v = 2   x   0,2 2,05   x   10 - 5 = 1,9   x   10 4

Esse é um regime laminar porque estamos abaixo do reynold crítico para uma placa plana que é Re = 5 x 105, sacou?

Então agora é só usar a correlação apropriada às condições dadas e encontrar o valor de hX=1m, e a correlação para Nusselt local é:

N u x = h x X K = 0,332   R e x 0,5 P r 1 / 3

h x = K X 0,332 R e x 0,5 P r 1 / 3 = 0,14 0,2 0,332   1,9   x   10 4 0,5   x   279 1 3 = 207,3 W m 2 ° C

Passo 2

Agora, simbora fazer a mesma ideia, mas para toda a placa, ok?

Calculamos de novo o valor de Reynold...

R e L = V L v = 2   x   0,5 2,05   x   10 - 5 = 4,9   x   10 4

Estamos em regime laminar, e agora vamos calcular o h médio usando a correlação apropriada ao tipo de regime e geometria de escoamento!

N u = h L K = 0,664 R e L 0,5 P r 1 / 3

h = K L 0,664 R e L 0,5 P r 1 / 3 = 0,14 0,5 x   0,664   x   4,9   x   10 4 0,5   x   279 1 3 = 262 W m 2 ° C

Passo 3

(b) Vamos agora usar a correlação de Churcill e Ozoe como é pedido no enunciado. MAS VOU PRECISAR FAZER TUDO DE NOVO? NÃOOOOOOOOOOOOOOOO!!!!

Como as condições se mantiveram, o valor de Reynold tanto local quanto médio se manterão iguais, o que mudará é a forma de calcular h, pois usaremos a correlação pedida, sacou?

N u x = h x X K = 0,3387 P r 1 / 3 R e x 0,5 1 + 0,0468 P r 2 3 1 4

h x = K X 0,3387 P r 1 / 3 R e x 0,5 1 + 0,0468 P r 2 3 1 4 = 0,14 0,2 x 0,3387   x   279 1 / 3   x   1,9   x   10 4 0,5 1 + 0,0468 279 2 3 1 4 = 211,5 W m 2 ° C

Bora agora calcular o h médio usando aquela fórmula que é integrando o hx em torno de toda a placa:

h = 1 L ∫ 0 L = 0,5 h x d X

h x = K X 0,3387 P r 1 / 3 R e x 0,5 1 + 0,0468 P r 2 3 1 4

Vamos abrir Reynold na forma de R e x = V X K e vamos ver como fica hx?

h x =   K 0,3387 P r 1 3 V v 0,5 X - 0,5 1 + 0,0468 P r 2 3 1 4

Pra gente não precisar ficar escrevendo todo esse treco enorme na integral, vamos pegar a parte que é constante, ou seja, que está associada as propriedades do fluido e chamaremos de C, então..

C = K 0,3387 P r 1 3 V v 0,5 1 + 0,0468 P r 2 3 1 4

Jogando na integral, teremos:

h = 1 L ∫ 0 L = 0,5 h x d X = 1 L ∫ 0 L = 0,5 C X - 0,5 d X = C L ∫ 0 L = 0,5 X - 0,5 d X

h = C L 0,5 0,5   L = 2 C L - 0,5

Substituindo C e L na equação de h médio e em seguida os valores das propriedades, vamos encontrar o valor de h.

h = 2 K 0,3387 P r 1 3 V v 0,5 1 + 0,0468 P r 2 3 1 4 x L - 0,5

h = 2   x   0,14 0,3387   x   279 1 3 2 2,05   x   10 - 5 0,5 1 + 0,0468 279 2 3 1 4 x 0,5 - 0,5 = 267 ,   4 W m 2 ° C

Resposta

  1. h x = 207,3 W m 2 ° C e h =   262 W m 2 ° C

  2. h x = 211,5 W m 2 ° C e h = 267 ,   4 W m 2 ° C
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um elemento aquecedor coberto com níquel, com uma espessura de 15 mm e uma condutividade térmica de 50W /( m · K ) , está exposto à água saturada a pressão atmosférica. Um termopar é fixado à sua supe
A energia térmica gerada por um chip de silício aumenta na proporção de sua velocidade de processamento. O chip de silício do Problema 10.23 é projetado para operar no regime de ebulição nucleada a ap
Etilenoglicol saturado a 1a t m é aquecido por uma superfície horizontal revestida de cromo, que tem um diâmetro de 200m m e é mantida a uma temperatura de 480K . Estime a potência de aquecimento exig
Um chip de silício com espessuraL=2,5m m e condutividade térmica k s=135W / ( m·K ) é resfriado pela ebulição de um fluorocarboneto líquido saturado ( T s a t=57 ° C ) sobre sua superfície. Os circuit
Um aparelho para efetuar experimentos de ebulição tem uma barra de cobre ( k=400W / ( m·K ) ) , que tem uma de suas extremidades exposta a um líquido em ebulição e um aquecedor elétrico encapsulado na