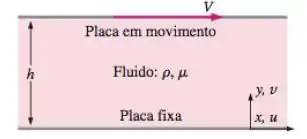
12. No capitulo 9 (Exemplo 9-15), nós geramos uma solução ‘’exata’’ da equação de Navier-stokes para escoamento Couette totalmente desenvolvido entre duas placas planas horizontais (Figura P10-12), com a gravidade agindo na direção negativa de z (para dentro da página da Figura P10-12). Usamos a pressão real nesse exemplo. Repita a solução para a componente x da velocidade u e pressão P, mas use a pressão modificada nas suas equações. A pressão é em . Mostre que você obtém o mesmo resultado de antes. Discuta.

Equação da hereditariedade:

De acordo com as hipóteses 1 e 6, respectivamente, v = 0 e w = 0.

Então, nossa equação de hereditariedade simplificada nos fornece:

Veja que esse resultado nos mostra que não é uma função de x, ou seja, o escoamento é totalmente desenvolvido.

Sabe o que isso significa?

Bom, quer dizer que ou escoamento independente da localização de origem. Além disso, como você não tem uma função de tempo nem z, temos que apenas uma função de y:

Equação do movimento:

Componente x:

Como o escoamento é estacionário, não há dependência em relação ao tempo

Componente y:

Componente z:

Ou seja, uma pressão modificada P 'não é função do nem z.

P 'também não é função do tempo, afirma essa hipótese (2).

Nem de x, como afirmado pela hipótese (5). Assim, podemos concluir que P 'é constante.

Agora, integramos duas vezes a simplificação do componente x da equação de movimento e vamos encontrar:

Onde C 1 e C 2 são constantes de integração!

Desta vez, aplicáveis ​​às condições de contorno pré-definidas, obtemos C 1, C 2 e C 3 :

CC3:

CC1:

CC2:

E substituído na equação da velocidade em x (u), obtendo, finalmente, o perfil de velocidade: