10. Considere escoamento Poiseuille permanente, incompressível, laminar e totalmente desenvolvido entre duas placas paralelas horizontais ( os perfis de velocidade e pressão são mostrados na Figura P10-10). Em alguma posição horizontal , a pressão varia linearmente com a distancia vertical , conforme mostra a figura. Escolha um plano de referencia apropriado (, desenhe o perfil da pressão modificada ao longo da fatia e escureça a região que representa a componente de pressão hidrostática. Discuta.
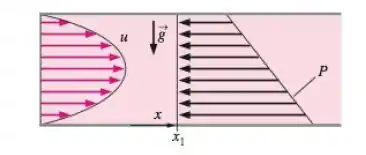
Passo 1
Como a maioria de nossos professores nos falam em sala, em todo e qualquer problema de mecânica dos fluidos nos temos que ‘’ amarrar’’ nossas soluções em hipóteses para que as mesmas façam sentido. Sendo assim para este problem temos as seguintes:
• Fluido incompressível.
• Escoamento totalmente desenvolvido.
• Gravidade não atua no sentido negativo do eixo z.
• Não há nenhuma superfície livre no sistema.
Passo 2
Por definição, uma pressão modificada P 'é a soma da pressão termodinâmica e da pressão hidrostática.
Então, adicionamos uma pressão hidrostática, gh, ao perfil de pressão P.
Assim, como a gravidade não atua no plano xz, uma pressão seria constante ao longo de qualquer fatia vertical.
Logo, podemos inferir que o aumento linear em P, da placa superior à inferior, deve ocorrer à pressão hidrostática.
Portanto, quando adicionamos gh a P, para obter uma pressão modificada, podemos observar que P 'fica nessa posição horizontal.
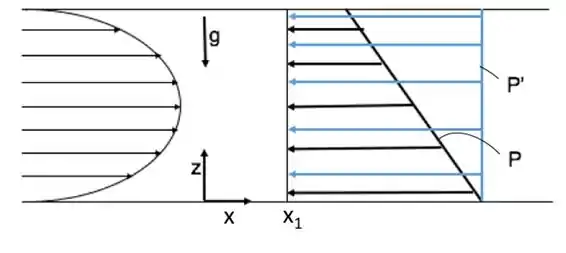 A região hachurada representa uma pressão hidrostática, gh. P 'é constante ao longo da fatia x = x 1 !
A região hachurada representa uma pressão hidrostática, gh. P 'é constante ao longo da fatia x = x 1 !
E como vantagens? Você sabe quais são?
Se usarmos a pressão modificada, ela poderá excluir o limite de gravidade da equação de Navier-Stokes, além de P ser a mais simples que P.
Resposta
Desenho e discussão em texto.