Exercícios de Equações de Navier-Stokes - Lista de Exercícios Resolvida

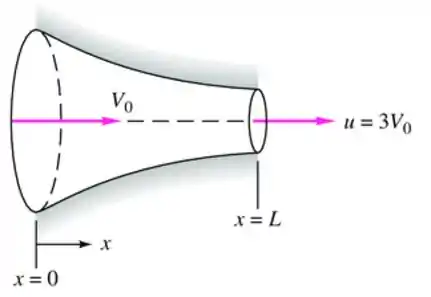
O escoamento pelo bocal convergente da Figura pode ser aproximado por uma distribuição de velocidades unidimensional

Encontre uma expressão geral para a aceleração do fluido no bocal.

Para o caso específico e , calcule a aceleração, em g’s, na entrada e na saída.

Um campo de velocidade bidimensional é dado por

em unidades arbitrárias. Em , calcule as acelerações e , o componente de velocidade na direção , a direção da velocidade máxima e a direção da aceleração máxima.

Um campo de escoamento incompressível, tridimensional, proposto tem a seguinte forma vetorial:

Determine se esse campo é uma solução válida para a continuidade e para Navier-Stokes. Se , encontre o campo de pressão .

Considere um escoamento permanente, bidimensional, incompressível, de um fluido newtoniano no qual o campo de velocidade é conhecido: , , . Esse escoamento satisfaz a conservação da massa? Encontre o campo de pressãose a pressão no pontoé igual a .

Considere o campo de velocidade no plano dado por:

Determine o número de dimensões do escoamento, se ele é um possível escoamento incompressível e a aceleração de uma partícula fluida no ponto .

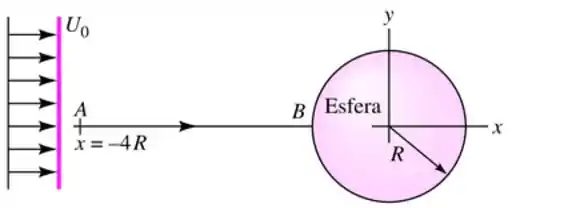
Considere a esfera de raio imersa em uma corrente uniforme , como mostra a Figura. De acordo com a teoria, a velocidade do fluido ao longo da linha de corrente é dada por

Encontre a posição da aceleração máxima do fluidod ao longo de e o tempo necessário para que uma partícula de fluido se desloque de a .

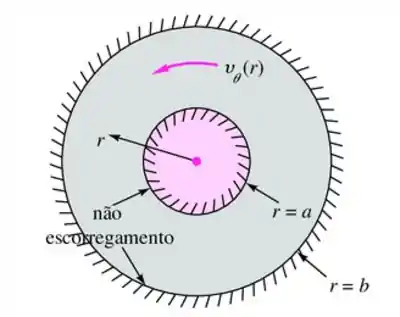
Das equações de Navier-Stokes para escoamento incompressível em coordenadas polares encontre o caso mais geral de movimento puramente circulatório , , para escoamento sem escorregamento entre dois cilindros concêntricos fixos, como na Figura.

Equação da continuidade em coordenadas cilíndricas:

Equações de Navier-Stokes em coordenadas cilíndricas:

Um campo de escoamento permanente, incompressível, sem atrito, é dado por

em unidades arbitrárias. Seja a massa específica e despreze a gravidade. Encontre uma expressão para o gradiente de pressão na direçãoo .