Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 21
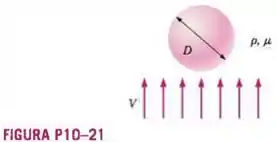
Uma gota de água em uma nuvem de chuva tem um diâmetro (Figura P10-21). A temperatura do ar é 25°C e sua pressão é a pressão atmosférica padrão. Com que rapidez o ar tem que se mover verticalmente para que a gota permaneça suspensa no ar?
Passo 1
Oi pessoal, tudo bem?
Primeiramente, assumimos que:
1. A queda é esférica.
2. A aproximação do fluxo rastejante é apropriada para a resolução do problema.
Bem, devemos encontrar a velocidade do ar para que a gota permaneça suspensa no ar, de acordo com os dados do problema, que são:
Obs: As propriedades da água e do ar à são encontradas na Tabela A-3 e A-9, respectivamente.
Passo 2
Como a “queda” da gota em relação ao ar deve ser nula, sua força descendente deve equilibrar exatamente com sua força ascendente, que no caso se refere à força exercida pelo ar. A força descendente é a força peso da partícula (sabendo que o volume de uma esfera é ):
Assim:
A força ascendente é a força aerodinâmica de arrasto que atua na partícula mais a força de flutuação na partícula.
Sabemos que força de arrasto sobre uma esfera em escoamento lento é , enquanto que a força de flutuação nada mais é do que a força peso do ar. Então:
Passo 3
Assim, para o equilíbrio, as forças ascendente e descendente devem ser iguais. Igualando as equações 1 e 2, temos:
Como queremos descobrir a velocidade, a isolamos:
Portanto:
Por fim, devemos verificar se o número de Reynolds é pequeno o suficiente para que a aproximação do escoamento lento seja apropriada:
E lembremos sempre que, desde que , a aproximação do escoamento lento é apropriada.
Resposta
Portanto: