Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 147

12-147 Repita o Problema 12-146 para o hélio.

Passo 1

Vamos relembrar o problema 12 - 146 !!

Tinhamos ar escoando em um duto quadrado, de dimensões 10 c m xx 10 c m e a gente queria encontrar overset(˙)(Q)_m á x e o problema falava pra desprezar as perdas por atrito!

O que vai mudar agora é que ao invés de ar temos hélio!

Consideramos que se o ar é aquecido e se tem transferência de calor, é do escoamento de Rayleigh que estamos falando! Sabendo também que a transferência de calor para quando M a = 1 , então M a_2 = 1 !!

Abaixo tem um esqueminha com outros dados do enunciado:

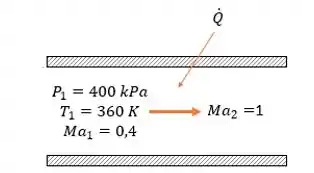
Para achar overset(˙)(Q)_m á x usamos:

overset(˙)(Q) = overset(˙)(m)_a r c_p (T_02 - T_01)

Não conhecemos overset(˙)(m)_a r , T_02 e T_01 , vamos atrás deles agora!!

Passo 2

overset(˙)(m)_a r é dado por:

overset(˙)(m)_h é l i o = rho_1 A_c 1 V_1

Se considerarmos o comportamento do hélio como gás ideal:

rho_1 = (P_1)/(R T_1)

Lembrando que R = 2,077 k J // k g K , podemos calcular rho_1 :

rho_1 = (400)/(2,077 xx 360) = 0,5350 k g // m^3

Falta V_1 :

V_1 = M a_1 c_1

Calculamos c_1 , lembrando que para o hélio k = 1,667 :

c_1 = sqrt(k R T_1) = sqrt(1,667 xx 2077 xx 360) = 1116 m // s

E V_1 :

V_1 = 0,4 xx 1116 = 446,6 m // s

E finalmente vamos achar overset(˙)(m)_a r :

overset(˙)(m)_a r = 0,5350 xx (0,1 xx 0,1) xx 446,6 = 2,389 k g // s

Passo 3

Para achar T_01 // T_0^* usamos a seguinte relação:

(T_01)/(T_0^*) = ((k + 1) M a_1^2 [2 + (k - 1) M a_1^2])/((1 + k M a_1^2)^2)

Substituindo:

(T_01)/(T_0^*) = ((1,667 + 1) 0,4^2 [2 + (1,667 - 1) 0,4^2])/((1 + 1,667 xx 0,4^2)^2) = 0,5603

Como M a_2 = 1 : (T_02)/(T^*) = 1

Podemos fazer:

((T_02)/(T^*))/((T_01)/(T^*)) = (T_02)/(T_01) = (1)/(0,5603)

Logo:

T_02 = 1,78 T_01

Considerando o escoamento é isentrópico, assim podemos achar T_01 :

T_01 = T_1 (1 + (k - 1)/(2) M a_1^2)

Substituindo e calculando:

T_01 = 360 xx (1 + (1,667 - 1)/(2) 0,4^2) = 379,2 K

Então:

T_02 = 1,78 xx 379,2 = 676,8 K

Passo 4

Podemos finamente achar overset(˙)(Q) :

overset(˙)(Q) = overset(˙)(m)_h c_p (T_02 - T_01)

lembrando que c_p é tabelado:

c_p = 5,193 k J // k g K

Substituindo:

overset(˙)(Q) = 2,389 xx 5,193 (676,8 - 379,2)

Calculando:

overset(˙)(Q) = 3690 k W

Uhuuuul!!!

Resposta

overset(˙)(Q)_m á x = 3690 k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água escoa rapidamente em um canal de 25 cm de profundidade. Ao se penetrar a superfície livre com a ponta de um lápis, forma-se uma onda a jusante em formato de cunha com um ângulo total de 38°. Calc
Pedras lançadas sucessivamente no mesmo ponto, dentro do escoamento de água em um canal com 65 cm de profundidade, criam duas ondas circulares, como na figura abaixo. Com base nessa informação, calcul
O canal em concreto finalizado da figura abaixo é projetado sem a barreira, para uma vazão de 6 m³/s a uma profundidade normal de 1 m. Determine (a) a declividade de projeto do canal e (b) a redução n
O escoamento laminar de drenagem do P10.12 pode passar por uma transição para a turbulência se R e500 . Se a declividade do pavimento for 0,0045, qual será a máxima espessura da camada, em milímetros,
Se a tensão superficial γ for incluída na analise do problema P10.9, a velocidade de onda resultante é c 0 2 = g λ 2 π + 2 π γ ρ λ tanh ⁡ 2 π y λ (a) Determine se essa expressão é afetada pelo número