Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 145
12-145 Ar é resfriado à medida que escoa através de um duto com 20 cm de diâmetro. As condições de entrada são , e e o número de Mach de saída é . Desprezando os efeitos do atrito determine a taxa de resfriamento do ar.
Passo 1
Vamos lá!! Aqui como consequência do escoamento a gente tem o resfriamento do ar e se tem transferência de calor, é do escoamento de Rayleigh que estamos falando!
Vamos fazer um esqueminha do problema:
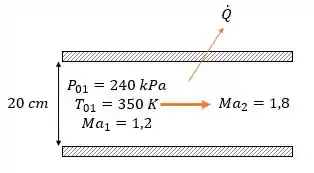
E queremos achar a taxa de resfriamento do ar, !
Para isso vamos usar a seguinte expressão:
Não conhecemos nem nem , então vamos atrás deles!!
Passo 2
é dado por:
Se considerarmos o comportamento do ar como gás ideal:
Considerando o escoamento é isentrópico, assim podemos achar :
Lembrando que para o ar :
Agora :
Substituindo:
Lembrando que , podemos calcular :
Ta falantando pra a gente conseguir calcular :
Calculamos :
E :
E finalmente vamos achar :
Calculando:
Passo 3
Agora precisamos de , usando e conseguimos relações importante na tabela :
Com isso podemos fazer:
E ficamos com:
Lembrando que
Passo 4
Podemos finamente achar :
lembrando que é tabelado:
Substituindo:
Calculando:
Uhuuuul!!!