Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 149

12-149 Ar a condições sônicas, temperatura e pressão estáticas de 500   K   e   420   k P a , respectivamente, deve ser acelerado até um número de Mach de 1,6 resfriando à medida que escoa através de um canal com área de seção transversal constante. Desprezando os efeitos do atrito, determine a transferência de calor do ar necessária em kJ/kg.

Resposta: 69,8 kJ/kg

Passo 1

Vamos lá!! Aqui como consequência do escoamento a gente tem o resfriamento do ar e se tem transferência de calor, é do escoamento de Rayleigh que estamos falando!

Vamos fazer um esqueminha do problema:

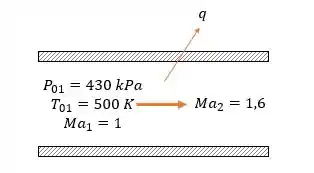
Queremos encontrar q , que pode ser calculado por:

q = c p T 02 - T 01

Precisamos encontrar T 02 e T 01 , então vamos nessa!!!!

Passo 2

Consultando a tabela A - 15 :

M a 1 = 1 → T 01 T * = 1

M a 2 = 1,6 → T 02 T * = 0 , 8842

Então podemos fazer:

T 02 T * T 01 T * = T 02 T 01 = 0,8843 1 = 0,8843

Logo:

T 02 = 0,8843   T 01

Considerando o escoamento é isentrópico, assim podemos achar T 01 :

T 01 = T 1 1 + k - 1 2   M a 1 2  

Lembrando que para o ar k = 1,4 :

T 01 = 500 × 1 + 1,4 - 1 2   1 2 = 600   K

Então:

T 02 = 0,8843 × 600 = 530,5   K

Passo 3

Podemos então calcular q :

q = c p T 02 - T 01

lembrando que c p é tabelado:

c p = 1,005   k J / k g   K

Substituindo:

q = 1005 530,5 - 600

Calculando:

q = - 68,8 k J k g

Uhuuuul!!!

Resposta

q = - 68,8 k J k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o canal do problema FE10.1, se a profundidade da água é de 2 m e a vazão de escoamento uniforme é de 24 m3/s, qual é o valor aproximado do coeficiente n de rugosidade de Manning?(a) 0,015, (b) 0,
O escoamento através do canal de água da figura abaixo tem uma superfície livre em três locais. Isso o qualifica como um escoamento em canal aberto? Explique. O que representa essa linha tracejada?
No problema P10.15, para concreto finalizado, determine a porcentagem na redução da vazão se o canal é dividido no centro pela barreira proposta nesse problema P10.15. Como sua estimativa mudará se as
Pedras lançadas sucessivamente no mesmo ponto, dentro do escoamento de água em um canal com 42 cm de profundidade, criam duas ondas circulares, como na figura abaixo. Com base nessa informação, calcul
(a) Para a drenagem laminar de uma camada fina e larga de água sobre um pavimento inclinado de um ângulo θ , como na figura P4.36, mostre que a vazão volumétrica é dada por: Q = ρ g b h 3 s e n θ 3 μ