Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 148

12-148 Ar é acelerado à medida que é aquecido em um duto com atrito desprezível. O ar entra a V 1   =   100   m / s ,   T 1   =   400   K   e   P 1   =   35   k P a e, em seguida, sai a um número de Mach de M a 2 = 0,8 . Determine a transferência de calor para o ar em kJ/kg. Determine também a quantidade máxima de transferencia de calor sem reduzir a vazão em massa do ar.

Passo 1

Vamos lá!! Aqui durante o escoamento a gente tem o ar sendo aquecido e se tem transferência de calor, é do escoamento de Rayleigh que estamos falando!

Aqui a gente tem um esqueminha do que ta acontecendo:

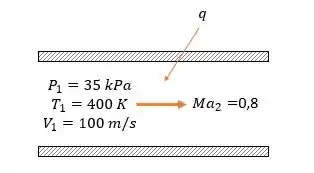
Queremos descobrir quem é   q para as condições dadas no enunciado e também q m á x !

Podemos encontrar q da seguinte forma:

q = c p T 02 - T 01

Agora, sabendo que a transferência de calor para quando M a = 1 , para q m á x sem que a vazão mássica do ar diminua, fazemos M a 2 = 1 !

Mas primeiro vamos nos concentrar em achar q , para isso precisamos de T 01 e T 02 !

Passo 2

Uma forma mais simples de achar T 01 e T 02 são as relações da tabela A - 15 , mas pra isso precisamos conhecer M a 1 e M a 2 !

Sabendo que:

M a 1 = V 1 / c 1

c 1 pode ser calculado:

c 1 = k R T 1

Sabendo que, para o ar R = 287   k J / k g   K e k = 1,4 :

c 1 = 1,4 × 287 × 400 = 400,9   m / s

Então temos:

M a 1 = 100 400,9 = 0,2494

Consultando a tabela A - 15 :

M a 1 = 0,2 494 → T 01 T * = 0,2559

M a 2 = 0,8 → T 02 T * = 0,9639

Podemos fazer:

T 02 T * T 01 T * = T 02 T 01 = 0,9639 0 , 2559 = 3,7667

Logo:

T 02 = 3,7667   T 01

Considerando o escoamento é isentrópico, assim podemos achar T 01 :

T 01 = T 1 1 + k - 1 2   M a 1 2  

Substituindo e calculando:

T 01 = 400 × 1 + 1,4 - 1 2   0,2494 2 = 405   K

Então:

T 02 = 3,7667 × 405 = 1526   K

Passo 3

Podemos então calcular q :

q = c p T 02 - T 01

lembrando que c p é tabelado:

c p = 1,005   k J / k g   K

Substituindo:

q = 1005 15 26 - 405

Calculando:

q = 1180 k J k g

Passo 4

Agora queremos q m á x :

q m á x = c p T 02 - T 01

As condições iniciais são iguais, então T 01 = 405   K , sabendo que, para M a 2 = 1 , T 02 / T * = 1 , então:

T 02 T * T 01 T * = T 02 T 01 = 1 0,2559 = 3,91

Então:

T 02 = 3,91 × 405 = 1583

Podemos calcular q m á x :

q m á x = 1005 1583 - 405

Calculando:

q m á x = 1180   k J / k g

Resposta

q = 1180   k J / k g

q m á x = 1180   k J / k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma engenheira faz medidas cuidadosas com um vertedouro (ver a seção 10.7) que monitora um canal de concreto sem acabamento com uma declividade de 1°. Ela constata, talvez com certa surpresa, que quan
Um canal de formato V revestido de tijolos de barro, com um ângulo total de 90°, tem 1 km de comprimento e um declive de 1:400. Quando operando a uma profundidade de 2m, a extremidade a montante é fec
Deseja-se escavar um canal em terra de seção transversal trapezoidal com θ = 60 ° (ver Figura 10.7). A vazão esperada é de 13, 5 m³/s, e a declividade é de 1,5 m por km. A profundidade do escoamento u
Um aqueduto trapezoidal (figura 10.7) tem b = 5 m e θ = 40 ° e tem uma vazão normal de 60 m³/s de água quando y = 3,2m . Para superfícies em tijolo de barro, calcule a queda de elevação necessária em
Um canal circular de concreto sem acabamento para água tem uma declividade de 1:600 e um diâmetro de 1,52 m. Avalie a vazão normal em litros/min para a qual a tensão cisalhante média na parede é 7,18