Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 130
130. Em um processo de secagem em uma fábrica de papel, uma folha de pasta de papel (uma mistura de água e fibra) possui uma velocidade linear de 5 m/s quando é enrolada. Aquecedores radiantes mantêm a temperatura da folha em Ts = 330 K, enquanto há evaporação da água para o ar ambiente seco e a 300 K, acima e abaixo da folha.
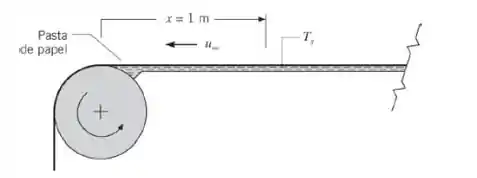
(a) Qual é o fluxo de evaporação a uma distância x = 1 m da aresta frontal do rolo? Qual é o valor correspondente do fluxo radiante (irradiação G) que deve ser fornecido à folha para manter a sua temperatura em 330 K? A folha tem uma absortividade α = 1.
(b) Para acelerar os processos de secagem e produção de papel, a velocidade e a temperatura da tira são aumentadas para 10 m/s e 340K, respectivamente. Para manter uma temperatura uniforme na tira, a irradiação G deve ser variada com x ao longo da tira. Para 0 ≤ x ≤ 1m, calcule e represente graficamente as variações de hm,x(x), (x) e G(x).
Passo 1
Calculando a temperatura média entre o ar e água primeiro ficamos com:
As propriedades do ar e da água serão coletadas nesta temperatura.
Da tabela A.15, obtemos as seguintes propriedades do ar a 315K:
Sendo assim, temos que a difusidade molecular de massa a é:
Passo 2
Letra (a)
Calcule o número de Reynolds dado por:
Como, o escoamente é laminar.
A partir daí basta calcularmos o número de Sherwood como:
Em que,
Substituindo:
Escrevendo uma outra relação para chegamos em:
Calcule a taxa média de secagem do papel.
O fluxo radiante pode ser calculado mediante a um balanço de energia:
Substituindo os valores temos que:
Passo 3
Letra (b)
Para o primeiro caso pedido temos o seguinte:
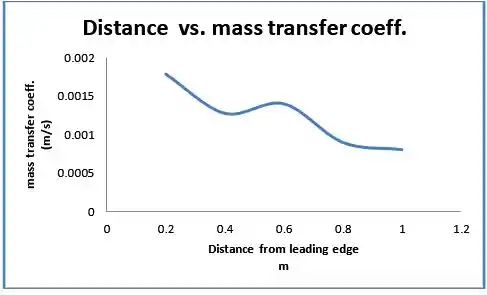
Para o segundo caso pedido temos o seguinte:
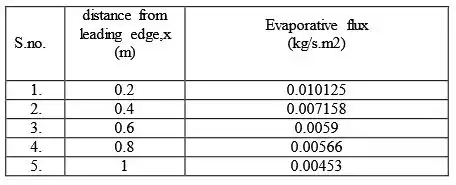
Para o terceiro caso pedido temos o seguinte:
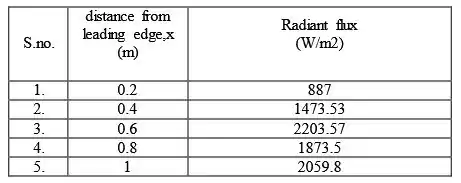
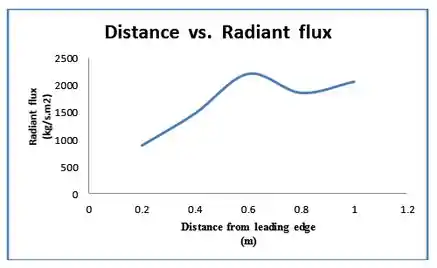
Resposta
- /
- Gráficos e tabelas