Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 116
13-116 Água escoa de modo uniforme a meia carga em um canal circular com 1,2 m de diâmetro assentado com uma inclinação de 0,004. Se a vazão da água for medida como 1,25 m³/s, determine o coeficiente de Manning do canal e o número de Froude.
Passo 1
Pra a gente começar com o pé direito, vamos desenhar um esqueminha do canal:
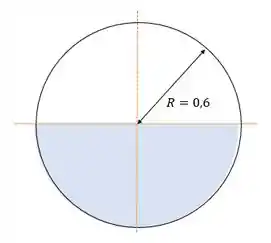
A gente conhece as dimensões do canal, a inclinaçã e sua vazão e queremos achar o coeficiente de Manning e o número de Froude!
Vamos começar pelo coeficiente de Manning, que a aparece na expressão para calcular a vazão:
Isolando :
Agora a gente só precisa ir atrás das outras icógnitas!!
Passo 2
A área transversal é a metade da área de uma circunferência, já que o canal opera em meia carga:
O raio hidráulico é dado pela razão da área e o perimetro, que nesse caso também é a metade do perímetro de uma circunferência:
Passo 3
O problema nos da e , lembrando que então:
Calculando:
Passo 4
Agora vamos calcular o número de Froude!!
A velocidade é dada por:
E o é a profundidade hidráulica:
Substituindo e calculando:
E como , então o escoamento é supercrítico!!