Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 45
O cálculo nos mostra que o ângulo de parede mais eficiente para um canal em V (Figura P10.41) é Ele produz a vazão normal mais alta para uma dada área. Mas esse ponto máximo é agudo ou achatado? Para uma área de escoamento de e um canal de concreto sem acabamento com uma declividade de 0,004, faça um gráfico de vazão normal Q, em , em função do ângulo para o intervalo e comente.
Passo 1
E lets go, lets go resolver essa!
Para um concreto sem acabamento,
Tendo para o canal em V,
O perímetro molhado é dado por:
Assim, o raio hidráulico,
e, a vazão
Substituindo tudo na expressão de vazão, teremos:
Passo 2
Bora utilizar algum software para plotar nosso gráfico com base nessa expressão que encontramos para a vazão, lembrando que estamos variando , assim:
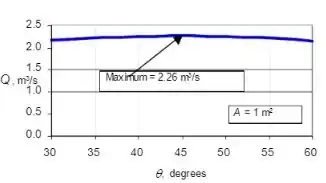
No gráfico conseguimos ver que em temos um máximo, tendo um ponto achatado!
Resposta
Ei, a resposta está no passo a passo :)