14-8 Uma bomba d'água aumenta a pressão da água que passa através dela (Figura P14-8). Estima-se que a água seja incompressível. Para cada um dos três casos listados abaixo, como a
velocidade média da água varia através da bomba? Em particular, é menor do que, igual a ou maior do que ? Mostre suas equações e explique.
- O diâmetro de saída é menor do que o diâmetro de entrada ;
- Os diâmetros de entrada e saída são iguais ;
- O diâmetro de saída é maior do que o diâmetro de entrada
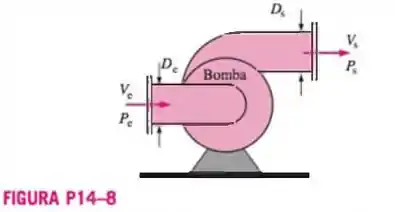
Passo 1
Vamos lá! Aqui a gente vai considerar um escoamento permanente e a água como fluído incompressível, beleza?!
A gente tem um esqueminha de uma bomba e queremos saber como varia a velocidade de acordo com os diâmetros da bomba em casos diferentes. Para isso a gente vai usar o princípio de conservação de massa:
Abrindo a equação, temos:
Sabendo que a área é dada por:
Substituindo:
Se a água é incompressível, então , cortando os termos em comum e isolando a
Passo 2
Temos uma relação entre velocidade e diâmetro, agora a gente vai analisar caso a caso!!
Na letra (a) , então a razão é maior que , logo .
Se , então a razão dos diâmetros é igual a e com isso na letra (b) .
Pra acabar, quando , então porque a razão dos diâmetros é menor que !
Resposta
- Para , então ;
- Para , ;
- Se , então .