Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 21
Água escoa a em um canal trapezoidal com largura inferior de . Os lados são inclinados a . Encontre a profundidade crítica para esse canal.
Passo 1
Vamos visualizar esse tal de canal trapezoidal para ficar mais fácil de montar a equação:
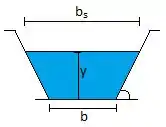
Hummm… Nosso exercício pede que há gente encontre a profundidade crítica, tá de boa! A gente consegue!
Vamos começar olhando para a fórmula que nos ajuda a encontrar a energia:
Essa equação pode ser escrita de outra, fazendo aparecer a vazão, já que foi ele que o enunciado nos deu:
Tá começando a ficar mais fácil de resolver, né?!
Passo 2
Visitando a tabela 11.1, temos como reescrever a área de escoamento, de forma que a gente tenha como encontrar ela:
Beleza! Agora é só substituir o na nossa equação da energia:
Opa! Seguindo para o próximo passo!
Passo 3
A gente não pode esquecer que o exercício quer os fatores críticos, então:
Agora podemos dar valores para até encontrar o que vai convergir, garantindo que o resultado da equação aqui de cima deve ser .
Passo 4
Vamos testar os valores de , lembrando que estamos trabalhando com as unidades em , então os fatores dados no exercício serão: e .
Já temos nossa profundidade crítica! Aeeee!!