Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 15

13-15 Água a 20°C escoa em um canal circular parcialmente cheio de 2 m de diâmetro a uma velocidade média de 2 m/s. Se a profundidade máxima da água for 0,5 m, determine o raio

hidráulico, o número de Reynolds e o regime do escoamento

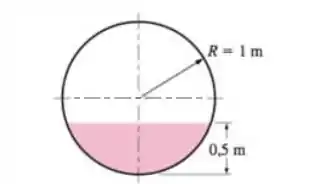
Passo 1

Vamos lá!! Queremos descobrir o raio hidráulico do nosso escoamento, o número de Reynolds e se ele é subcrítico, crítico ou supercrítico!

Vamos por partes então, começando pelo raio hidráulico, que é calculado por:

R h = A c p = θ - sin ⁡ θ cos ⁡ θ 2 θ R

Onde A c é a área de secção transversal e p   é o perímetro molhado! Para ajudar a gente, temos esse esqueminha:

cos ⁡ θ = R - a R = 1 - 0,5 1 = 0,5

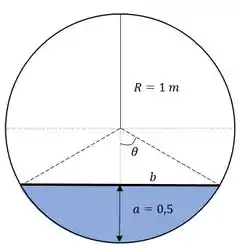
Mas queremos saber quem é θ :

cos - 1 ⁡ θ = 0,5

Achamos:

θ = π 3

Podemos então calcular R h :

R h = π / 3 - sin ⁡ π / 3 cos ⁡ π / 3 2 π / 3 × 1

Calculando:

R h = 0,293   m

Passo 2

Agora vamos calcular Reynolds:

Lembrando que para canais abertos o escoamento é turbulento quando R e > 500 .

R e = ρ V R h μ

Para água a 20 ℃ temos ρ = 998   k g / m 3 , μ = 1,002 × 10 - 3 k g / m s .

Substituindo: R e = 998 × 2 × 0,2 93 1,002 × 10 - 3 = 5,89 × 10 - 5

Logo o escoamento é turbulento!

Passo 3

Agora vamos ver se ele é subcrítico, crítico ou supercrítico, para isso usamos o número de Froude:

F R = V g y h

Mas:

y h = A c b = R 2 ( θ - sin ⁡ θ cos ⁡ θ ) 2 R sin ⁡ θ

Substituindo:

y h = 1 2 ( π / 3 - sin ⁡ π / 3 cos ⁡ π / 3 ) 2 sin ⁡ π / 3 = 0,3546

Se g = 9,81 m / s 2 :

F R = 2 9,81 × 0 , 3546 = 1,07

Se F R > 1 então o escoamento é supercrítico!

Resposta

R h = 0,293   m

R e = 5,89 × 10 - 5

Escoamento supercrítico!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Inicialmente um gás a uma velocidade supersônica entra em um duto convergente adiabático. Discuta o modo como isso afeta (a) a velocidade, (b) a temperatura, (c) a pressão e (d)a massa específica do f
Nitrogênio entra era um trocador de calor com escoamento constante a 150k P a , 10 ℃ ℃ e 100m / s , e recebe calor na quantidade de 120k J / k g à medida que escoa através dele. Onitrogênio sai do tro
Dióxido de carbono imóvel a 800 kPa e 400 K é acelerado de forma isentrópica até um número de Mach de 0,6. Determine a temperatura e pressão do dióxido de carbono após a aceleração
Inicialmente um gás a uma velocidade subsônica entra em um duto convergente adiabático. Discuta o modo como isso afeta (a) a velocidade, (b) a temperatura, (c) a pressão e (d) a.massa específica do fl
Calcule a temperatura, pressão e massa específica críticas do (a) ar a 200k P a ,100 ° C e 250m / s e (B) hélio a 200k P a ,40 ° C e 300m / s .