Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 20

Nitrogênio entra era um trocador de calor com escoamento constante a 150   k P a , 10 ℃ e 100   m / s , e recebe calor na quantidade de 120   k J / k g à medida que escoa através dele. O

nitrogênio sai do trocador de calor a 100   k P a com uma velocidade de 200   m / s . Determine o número de Mach do nitrogênio na entrada e na saída do trocador de calor.

Passo 1

Pra começar, vamos montar um esqueminha da situação que o enunciado ta dando pra a gente!

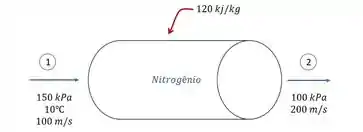
Temos o trocador de calor e a partir desses dados queremos achar o número de Mach na entrada e na saída do trocador, para isso vamos usar essa fórmula aqui:

M a = V c

Temos a velocidade do fluido tanto na entrada quanto na saída, mas não temos c que é a velocidade do som, para calcular c , temos:

c = k R T

Logo:

M a = V k R T

k e R são dados tabelados:

k = 1,4

R = 0,2968   k J / K g × K

E temos a temperatura de entrada

, mas não temos a temperatura de saída! O que podemos fazer então?!

Bem, a gente tem a quantidade de calor que o fluido recebe, q = 120   k J / k g !

O balanço de energia do trocador de calor pode ser escrito como:

q = c p T 2 - T 1 + V 2   2 - V 1     2   2

Opa, c p a gente pode conseguir olhando em uma tabela, temos q ,   T 1 e as velocidades V 1 e V 2 , podemos então isolar T 2 e calcular!

T 2 = 1 c p   q - V 2   2 - V 1     2   2 + T 1

Passo 2

Sabendo que, c p = 1,040 k J k g × K , substituindo:

T 2 = 1 1,040 × 10 3   120 × 10 3 - 200 2 - 100 2 2 + 10 = 110,96

T 2 ≅ 111 ℃

ATENÇÃO, quando alguma variável tem unidade de k J a gente tem que multiplicar por 10 3 para transformar em J !

Passo 3

Agora vamos enfim vamos calular os número de Mach!

M a = V k R T

Começando com M a 1 com T 1 = 10 ℃ = 283   K

M a 1 = 100 1,4 × 0,2968 × 10 3 × 28 3   = 0,292

Agora M a 2 com T 2 = 111 ℃ = 384   K

M a 2 = 100 1,4 × 0,2968 × 10 3 × 384   = 0 , 501

Prontinho!!!

Resposta

M a 1 = 0,292

M a 2 = 0,501

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ondas de superfície são causadas pela forma do objeto que toca apenas na superfície de uma corrente de escoamento de água, formando o padrão de onda mostrado. A profundidade da corrente é 150 mm. Dete
Verifique a equação dada na Tabela 11.1 para o raio hidráulico de um canal trapezoidal. Trace o gráfico da taxa R / y para b = 2m com inclinações do lado de 30° e 60° para 0,5my3m .
Ondas capilares (ondulações) têm pequena amplitude e comprimento de ondas, e são comumente vistas, por exemplo, quando um inseto ou uma pequena partícula atinge a superfície da água. Elas são ondas ge
O número de Froude caracteriza escoamento com uma superfície livre. Trace um gráfico, em escala logarítmica, da velocidade versus a profundidade para 0,1m / sV3m / s e 0,001my1m ; Trace a linha de F r
A solução das equações diferenciais completas para o movimento de ondas em líquidos em repouso, incluindo os efeitos da tensão superficial, mostra que a velocidade da onda é dada por: c = g λ 2 π + 2