13-81C Desenhe um diagrama de energia específica de profundidade para o escoamento das comportas submersas, e indique o escoamento através da comporta para os seguintes casos: (a) comporta sem atrito, (b) comporta basculante com escoamento de saída livre e (c) comporta basculante com escoamento afogado (incluindo o salto hidráulico de volta ao

Vamos lá desenhar nosso diagrama!!!

A gente tem situações, na primeira temos um escoamento que vai passar pela comporta e não vai ter perca por atrito. Na segunda temos com isso a saída é livre e na terceira a saída é submersa, ou seja . Lembrando que é a altura da abertura!

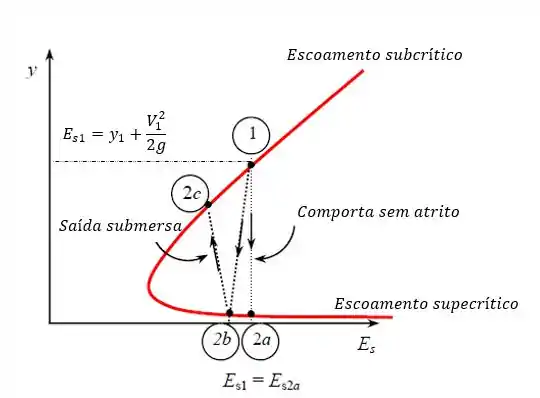
Como podemos perceber, quando não temos perda por atrito a energia mecânica se mantêm constante!

Agora, quando a superfície é livre eu tenho uma perda de energia associada a redução da produndidade do escoamento, é o caso , esse era o comportamento esperado porque não temos um salto hidráulico aqui, o escoamento passa de subcrítico para supercítico!

E por fim temos que representa a terceira situação! Nesse caso o escoamento passa de supercrítico para subcrítico e temos o aumento da profundidade do escoamento associada ao choque hidráulico!!

Belezinha?!