142. Passagens aletadas são frequentemente formadas entre placas paralelas para melhorar a transferência de calor por convecção no núcleo de trocadores de calor compactos. Uma importante aplicação é no resfriamento de equipamentos eletrônicos, onde uma ou mais estantes de aletas, resfriadas a ar, são colocadas entre componentes eletrônicos que dissipam calor. Seja uma única estante de aletas retangulares, com comprimento L e espessura t, com condições de transferência de calor por convecção correspondente a h e T∞.

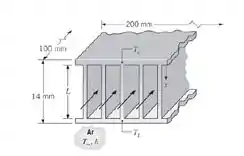
(a) Obtenha expressões para as taxas de transferência de calor nas aletas, qa,e e qa,L, em termos das temperaturas nas extremidades, Te e TL.

(b) Em uma aplicação específica, uma estante de aletas, com 200 mm delargura e 100 mm de profundidade, contém 50 aletas de comprimentoL = 12 mm. A estante completa é feita em alumínio e todas as placas possuem espessura de 1,0 mm. Se limitações de temperatura associadas aos componentes elétricos fixados às placas opostas ditam que as temperaturas máximas permitidas nestas placas são de Te = 400K e TL = 350 K, quais são as dissipações máximas de potência correspondentes se h = 150 W/(m2 · K) e T∞ = 300 K?

Letra(a)

Considere a solução geral para a distribuição de temperatura da aleta da seguinte forma:

Aqui,, C1e C2 são constantes, m é um parâmetro.

Considere a seguinte condição de limite em :

Aplique a condição de limite à solução geral da seguinte maneira:

Considere a condição de contorno da seguinte maneira:

Aplique a condição de contorno à solução geral.

Resolva as equações (1) e (2) para obter os valores de e .

Substitua os valores de e  na solução geral para obter a distribuição de temperatura.

Diferencie a expressão dos dois lados:

Considere a taxa de transferência de calor da lei de condução de Fourier da seguinte forma:

Substitua 0 por x .

Portanto, a expressão para a taxa de transferência de calor da aleta em  é .

Substitua L por x .

Portanto, a expressão para a taxa de transferência de calor da aleta em  é