Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 149

Água é aquecida em um tanque com tubos submersos de cobre, com paredes delgadas e diâmetro de 50   m m , nos quais escoam gases de combustão ( T g   =   750   K ) . Para melhorar a transferência de calor para a água, quatro aletas planas de seção transversal uniforme, em forma de cruz, são inseridas no interior de cada tubo. As aletas têm 5   m m de espessura e também são construídas em cobre ( k   =   400   W / ( m   ·   K ) ) .

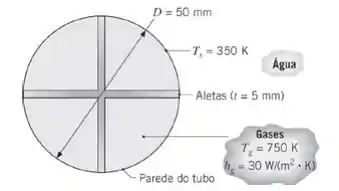
Sendo a temperatura na superfície do tubo igual a T s   =   350   K e o coeficiente de transferência de calor por convecção no lado do gás h g   =   30   W / ( m 2 ·   K ) , qual é a taxa de transferência de calor para a água por metro de comprimento do tubo?

Passo 1

Vamos para mais uma questão 😊. Aqui nós temos o diâmetro e a configuração interna da aleta de tubos de cobre submersos em água. Além da temperatura da parede do tubo e o coeficiente de temperatura e convecção do fluxo de gás através do tubo.

Com isso, vamos calcular a taxa de transferência de calor por comprimento do tubo, beleza? Então vamos lá \o/

Passo 2

Para resolver essa questão vamos assumir que:

(1) Estamos em condição de estado estacionário;

(2) A condução de aleta é unidimensional;

(3) As propriedades são constantes;

(4) A radiação é desprezível;

(5) O coeficiente de convecção é uniforme;

(6) A parede do tubo pode ser desdobrada e representada como uma parede plana com quatro aletas retas e retangulares, cada uma com uma ponta adiabática (já que, por simetria,pode haver fluxo de calor ao longo das aletas onde elas cruzam).

A taxa de transferência de calor por unidade de comprimento do tubo é:

q t ' = o h A ' t ( T g - T s )

Onde,

o = 1 - N A ' f A ' t ( 1 - f )

E, N A f ' = 4 × 2 L = 8 0,025 m = 0,20 m

A ' t = N A ' f + A ' b = 0,20 m + π D - 4 t = 0,20 m + π × 0,05 m - 4 × 0,005 m = 0,337 m

Passo 3

Para uma ponta de aleta adiabática,

f = q f q m a x = M tanh ⁡ m L h ( 2 L . 1 ) ( T g - T s )  

Onde,

M = h 2 l m + t k l m × t 1 2 T g - T s

Substituindo os valores:

M ≈ 30 W m 2 . K 2 m 400 W m . K 0,005 m 2 1 2 400   K = 4382   W  

E,

m L = h 2 l m + t k l m × t 1 2 L ≈ 30 W m 2 . K 2 m 400 W m . K 0,005 m 2 1 2 0,025 m = 0,137

Então, tanh ⁡ m L = 0,136 , e:

f = 4382   W 0,136 30 W m 2 . K ( 0,05 m 2 ) ( 400 K ) = 595 W 600 W = 0,992

o = 1 - 0,20 0,337 1 - 0,99 2 = 0.99 5

q t ' = 0,995 30 W m 2 . K 0,337 m 400 K = 4025   W / m

Resposta

q t ' = 4025   W / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Como um meio para aumentar a transferência de calor em circuitos integrados (chip) lógicos de alto desempenho, é comum a fixação de um dissipador de calor à superfície do chip, com o objetivo de aumen
Um chip de silício isotérmico, com um lado de comprimento W=20m m , encontra-se soldado a um dissipador de calor de alumínio ( k=180W / ( m·K ) ) com comprimento equivalente. O dissipador tem uma base
Uma aleta anular de alumínio com perfil retangular está fixada a um tubo circular que possui um diâmetro externo de 25m m e uma temperatura superficial de 250 ° C . A aleta possui 1m m de espessura e
É proposto resfriar com ar os cilindros de uma câmara de combustão através da fixação de um revestimento de alumínio com aletas anulares ( k=240W / ( m·K ) ) à parede do cilindro ( k=50W / ( m·K ) ) .
35 - Um componente eletrônico na forma de um disco com 20m m de diâmetro dissipa 100W quando montado sobre um grande bloco de uma liga de alumínio (2024), cuja temperatura é mantida a 27℃ ℃. A configu