Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 17

17. Um aparelho para medir condutividade térmica emprega um aquecedor elétrico que é posicionado entre duas amostras idênticas, com 30 mm de diâmetro e 60 mm de comprimento, que são pressionadas entre placas que são mantidas a uma temperatura uniforme To = 77°C, por um fluido circulante. Uma graxa condutora é colocada entre todas as superfícies para garantir um bom contato térmico. Termopares diferenciais, espaçados de 15

mm, são instalados no interior das amostras. As superfícies laterais das amostras são isoladas de modo a garantir transferência de calor unidimensional através das amostras.

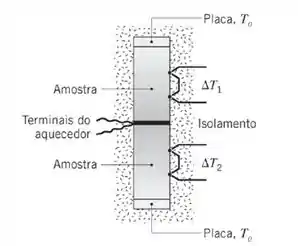
(a) Com duas amostras de aço inoxidável 316 no aparelho, a corrente elétrica no aquecedor é de 0,353 A a 100 V, e os termopares diferenciais indicam ΔT1 = ΔT2 = 25,0°C. Qual é a condutividade térmica do aço inoxidável das amostras? Qual é a temperatura média das amostras? Compare seu resultado com o valor da condutividade térmica para este material fornecido na Tabela A.1.

(b) Por engano, uma amostra de ferro Armco foi colocada na posição inferior do aparelho. Na posição superior permanece a amostra de aço inoxidável 316 utilizada no item (a). Para essa situação, a corrente no aquecedor é de 0,601 A a 100V, e os termopares diferenciais indicam ΔT1 = ΔT2 = 15,0°C. Quais são a condutividade térmica e a temperatura média da amostra de ferro Armco?

(c) Qual é a vantagem em se construir o aparelho com duas amostras idênticas imprensando o aquecedor ao invés de construí-lo com uma única combinação aquecedor-amostra? Quando a perda de calor pelas superfícies laterais das amostras se tornaria significativa? Em quais condições você esperaria ΔT1 ≠ ΔT2?

Passo 1

Letra (a)

Para o caso a, identifica-se que as amostras são idênticas da forma térmica passarão igualmente, o que é igual à metade da energia do aquecedor.

Calcule a potência do aquecedor que passa por cada amostra da seguinte maneira:

q = 1 2 V I

q = 1 2 100 × ( 0,353 )

= 17,65   W

Calcule a área da seção transversal das amostras de aço.

A c = π 4 D 2

A c = π 4 × 30   m m × 10 - 3 m 1   m m 2

= 0,7854 × 900 × 10 - 6 m 2

= 7,07 × 10 - 4   m 2

Calcular a condutividade térmica  K dos materiais de amostra de aço inoxidável.

q = k A c ∆ T ∆ x

k = q ∆ x A c ∆ T

Aqui, consideramos a diferença de temperatura para que você possa obter unidades de diferença de temperatura em graus centígrados ou em kelvin.

k = 17,65 × 15 × 10 - 3 7,07 × 10 - 4 × 25

k = 15 W m .   K

Portanto, a condutividade térmica do material de amostra de aço inoxidável é  15 W m .   K .

Calcule a queda de temperatura em todo o comprimento da amostra SS316.

T q u e d a = ∆ T 1 L ∆ x

T q u e d a = 25 × 60 15

= 100 ° C

Calcule a temperatura do aquecedor da seguinte maneira:

T h = T q u e d a + T 0

Aqui,  T q u e d a   está a queda de temperatura em todo o comprimento da amostra SS316 e  T 0   a temperatura é uniforme e  T h   é a temperatura do aquecedor.

T h = 100 + 77

T h = 177 ° C

Calcular a temperatura média das amostras.

T - = T h + T 0 2

T - = 177 + 77 2

= 127 ° C

= 400   K

Portanto, a temperatura média das amostras é  127 ° C .

Obtenha a condutividade térmica do aço inoxidável AISI 316 na tabela A.1 “(Propriedades termo-físicas de sólidos metálicos selecionados)” à temperatura  400   K .

k = 15,2 W m . K

Quando comparados, o valor da condutividade térmica da amostra   k = 15 W m . K  com o valor da tabela A.1 no valor da temperatura  400   K , as condutividades térmicas são quase iguais, portanto parece ser um bom acordo.

Passo 2

Letra (b)

Calcule a condutividade térmica  k s s   do material de amostra de aço inoxidável da seguinte maneira:

q = k s s A c ∆ T ∆ x

k s s = q ∆ x A c ∆ T

k s s = 17,65 × 15 × 10 - 3 7,07 × 10 - 4 × 25

k s s = 15 W m .   K

Calcule a taxa de calor de condução do material de amostra de aço inoxidável.

q s s = k s s A c ∆ T 1 ∆ x 1

q s s = 15 × 7,07 × 10 - 4 × 15 15 × 10 - 3

= 0,0106 × 10 3

= 10,6   W

Calcule a potência do aquecedor.

q h = V I

q h = 100 × 0,601

Calcule a taxa de condução de calor através da amostra de ferro Armco.

q = q h - q s s

q = 49,5   W

Calcule a condutividade térmica  k f e r r o   da amostra de ferro Armco.

q = k f e r r o A c ∆ T 2 ∆ x 2

k f e r r o = q ∆ x 2 A c ∆ T 2

k f e r r o = 49,5 × 15 × 10 - 3 7,07 × 10 - 4 × 15

= 70 W m . K

Portanto, a condutividade térmica da amostra de ferro Armco é  70 W m . K .

Calcule a queda de temperatura em todo o comprimento da amostra de ferro.

T q u e d a = ∆ T 2 L ∆ x 2

T q u e d a = 1 5 × 60 15

= 6 0 ° C

Calcule a temperatura do aquecedor da seguinte maneira:

T h = T q u e d a + T 0

Aqui,  T q u e d a   está a queda de temperatura em todo o comprimento da amostra SS316 e  T 0   a temperatura é uniforme e  T h   é a temperatura do aquecedor.

T h = 6 0 + 77

T h = 13 7 ° C

Calcular a temperatura média das amostras.

T - = T h + T 0 2

T - = 13 7 + 77 2

= 10 7 ° C

= 38 0   K

Portanto, a temperatura média das amostras é  10 7 ° C .

Passo 3

Letra (c)

A vantagem na construção do aparelho com duas amostras idênticas imprensando o aquecedor é que a energia elétrica total dissipada da unidade do aquecedor é compartilhada igualmente entre as duas amostras SS316.

Se você usar o aparelho com uma combinação de amostras de aquecedor único, mesmo que o aquecedor esteja bem isolado na parte traseira, o calor poderá ser dissipado, resultando em imprecisão nos cálculos.

Se a condutividade térmica do material isolante for aproximadamente comparável à condutividade térmica do material da amostra, a perda de calor das amostras de formato cilíndrico, especialmente das superfícies laterais, será significativa.

Para isolamento inadequado ao longo das superfícies laterais das amostras, o vazamento de calor dessas superfícies laterais leva à condição  ∆ T 1 ≠ ∆ T 2 .

Resposta

  1. 127 ° C             k s s = 15 W m .   K
  2. k f e r r o = 70 W m . K                       10 7 ° C
  3. Explicação em texto
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um aparelho para medir condutividade térmica emprega um aquecedor elétrico que é posicionado entre duas amostras idênticas, com 25m m de diâmetro e 60m m de comprimento, que são pressionadas entre pla
Uma panela é usada para ferver água. Ela é colocada sobre um fogão, a partir do qual calor é transferido a uma taxa fixa q o . Há dois estágios no processo. No Estágio 1, a água é levada de sua temper
Considere uma parede plana com 1 2 0m m de espessura e condutividade térmica igual a 1 2 0W / ( m · K ) . Sabe-se que há condições de regime estacionário quando T 1 = 5 00K e T 2 = 7 00K . Determine o
Considere uma janela com 400m m × 400m m em um avião. Para uma diferença de temperaturas de 90 ° C entre as superfícies interna e externa da janela, calcule a perda térmica através de janelas com L =
Um método para determinar a condutividade térmica k e o calor específico c p de um material está ilustrado na figura. Inicialmente, as duas amostras idênticas, de diâmetro D = 5 0m m e espessura L = 1