Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 2.Problemas - Ex. 7
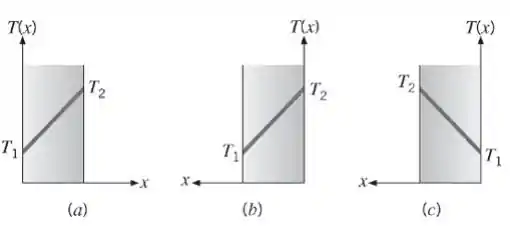
Considere uma parede plana com de espessura e condutividade térmica igual a . Sabe-se que há condições de regime estacionário quando e . Determine o fluxo térmico e o gradiente de temperatura para os sistemas de coordenadas mostrados.
Passo 1
Aqui, teremos que analisar cada caso separadamente, então, bora lá!
Letra a)
Calculando o gradiente de temperatura:
Calculando o fluxo de calor:
Passo 2
Letra b)
Calculando o gradiente de temperatura:
Calculando o fluxo de calor:
Passo 3
Letra c)
Calculando o gradiente de temperatura:
Calculando o fluxo de calor:
Te espero na próxima questão!
Resposta
Exercícios de Livros Relacionados
Calor é gerado uniformemente a uma taxa de 4,2 ⋅ 10 6W / m 3 em uma esfera ( k = 45W / m ⋅ K ) com 24 cm de diâmetro. A esfera é exposta à água fria a 0 °C com coeficiente de transferência de calor de
Considere uma casca esférica de raio interno r 1 e raio externo r 2 cuja condutividade térmica varia linearmente no intervalo específico de temperaturas, com k T = k 0 1 + β T , onde k 0 e β são duas
Considere uma casca cilíndrica de comprimento L, raio interno r 1 e raio externo r 2 cuja condutividade térmica varia linearmente no intervalo específico de temperaturas, com k T = k 0 1 + β T , onde
Em uma laje comprida de largura W (na direção do fluxo de calor, x) e espessura Z, ocorre condução de calor unidimensional permanente. A condutividade térmica da laje varia com a temperatura, k = k *
Uma parede plana de espessura 2L = 50 mm e condutividade térmica constante k = 8W / m ⋅ K gera calor uniformemente a uma taxa de e ˙ g e r . Sob condições permanentes, a distribuição de temperatura na