Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 2.Problemas - Ex. 15

Um método para determinar a condutividade térmica k e o calor específico c p de um material está ilustrado na figura. Inicialmente, as duas amostras idênticas, de diâmetro D = 5 0   m m e espessura L = 10   m m , e o aquecedor delgado se encontram a uma temperatura uniforme T i = 23,00 ° C , enquanto envolvidos por um pó isolante térmico. Em um dado instante, o aquecedor é energizado, fornecendo um fluxo térmico uniforme q o ' ' em cada uma das interfaces das amostras, que é mantido constante por um período de tempo Δ t o . Imediatamente após o início do aquecimento, a temperatura nesta interface, T o , está relacionada com o fluxo térmico através da expressão:

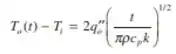
Em determinado teste, o aquecedor elétrico dissipa uma potência de 20,0   W durante um período de Δ t o = 1 0 0   s e a temperatura na interface, após 6 0   s de aquecimento, é T o ( 6 0   s ) = 2 6 , 7 7 ° C . Passado um longo intervalo de tempo após o desligamento do aquecedor, t ≫ Δ t o , as amostras atingem a temperatura uniforme de T o ( ∞ ) = 3 9 , 8 0 ° C . A massa específica do material das amostras, determinada através de medidas de volume e massa, é de m = 78   g .

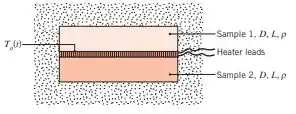
Determine o calor específico e a condutividade térmica do material testado. Olhando os valores das propriedades termo físicas nas Tabelas A.1 e A.2, identifique o material das amostras testadas.

Passo 1

E aí, tá pronto pra resolvermos essa questão?

Se ajeita aí e bora lá!

Começamos o nosso problema aplicando um balanço de energia no nosso sistema:

∆ E = E e n t - E s a i

Abrindo a nossa equação, temos:

P ∆ t o - 0 = m c p T ∞ - T i

Isolando o calor específico:

c p = P ∆ t o m T ∞ - T i

Substituindo os dados:

c p = 20 ⋅ 100 2 ⋅ 0,078 ⋅ ( 39,80 - 23,00 )

c p = 763   j / k g ⋅ K

Passo 2

Para calcularmos a condutividade térmica, temos que rearranjar a equação dada pelo enunciado:

k = t π ρ c p 2 q o ' ' T o t - T i 2

Calculando q o ' ' :

q o ' ' = P 2 A s = 4 P 2 π D 2 = 4 ⋅ 20 2 ⋅ π ⋅ 0,05 2

q o ' ' = 5093   W / m 2

Calculando ρ :

ρ = m V = 4 m π D 2 L = 4 ⋅ 0,078 π ⋅ 0,05 2 ⋅ 0,01

ρ = 3972,5   k g / m 3

Calculando k :

k = 60 π ⋅ 3972,5 ⋅ 763 ⋅ 2 ⋅ 5093 26,77 - 23,00 2

k = 46   W / m ⋅ K

Passo 3

Pelas propriedades obtidas, analisando as Tabelas A.1 e A.2, percebemos que estamos trabalho com o material Óxido de Alumínio Safira.

Te espero na próxima questão!

Resposta

c p = 763   j / k g ⋅ K

k = 46   W / m ⋅ K

Óxido de Alumínio Safira.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Gases de exaustão de uma fábrica estão sendo expelidos pela chaminé de exaustão de 10 m de altura, 1 m de diâmetro externo, 10 cm de espessura da parede e condutividade térmica de 40W / m ⋅ K . Os gas
Uma parede plana de espessura L = 4 cm tem condutividade térmica k = 20W / m ⋅ K . Uma reação química ocorre dentro da parede, resultando na geração de calor uniforme e uma taxa de e ˙ g e r = 10 5W /
Um tanque esférico de 5 m de diâmetro está cheio de oxigênio líquido ( ρ = 1141k g / m 3 , c p = 1,71k J / k g ⋅ ° C ) a -184 °C. Observa-se que a temperatura do oxigênio aumenta para -183 °C em um pe
Considere duas paredes, A e B, com as e mesmas áreas e com as mesmas quedas de temperatura através da espessura. A razão das condutividades térmicas é k A / k B = 4 , e a razão de espessuras das pared
O fluxo térmico que é aplicado na face esquerda de uma parede plana é q x " = 20W / m ² ². A parede tem espessura igual a L = 10m m e sua condutividade térmica é k = 12W / ( m.K ) . Se as temperaturas