Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 79
Ar a 20°C flui com velocidade V = 80,0 m/s sobre uma placa plana lisa de comprimento L = 17,5 m. Faça um gráfico do perfil da camada limite turbulenta em variáveis físicas (u em função de y) na distância x = L. Compare o perfil gerado pela lei da potência um sétimo, pela lei logarítimica e pela lei da parede de Spalding, supondo que a camada limite é completamente turbulenta desde o início da placa.
Passo 1
Fala aí, tudo bem? Vem comigo que eu vou te ajudar a interpretar o enunciado e resolver esse problema!
Aqui nessa questão a gente tem uma placa plana por onde escoa ar a , onde a camada limite é completamente turbulenta desde início da placa.
Devemos, então, traçar gráficos da velocidade em função da altura , a partir de três abordagens de equações diferentes: a lei da potência um sétimo, pela lei logarítmica e pela lei da parede de Spalding.
Essas três abordagens são dadas pelas seguintes equações:
- Lei da potência um sétimo
- Lei logarítimica
- Lei da parede de Spalding
- Lei da potência um sétimo
- Lei logarítimica
- Lei da parede de Spalding
Sendo a velocidade média do ar e a espessura da camada limite.
Para utilizar essa lei, nós devemos calcular a espessura da camada limite a partir da seguinte equação:
Sendo e constantes e é a viscosidade cinemática do ar a .
Além disso, é a velocidade de atrito, calculada a partir da equação:
Sendo que , e têm os mesmos valores que para a lei logarítmica.
Pronto, agora vem comigo que a gente vai resolver essa questão juntos!
Passo 2
Nesse passo, a gente vai calcular todas propriedades que a gente vai utilizar no próximo passo pra resolver a questão.
Primeiro, vamos começar com o número de Reynolds para uma distância de da placa. Pra calculá-lo, basta que a gente utilize a seguinte equação:
Agora, podemos calcular tanto a espessura da camada limite quanto a velocidade de atrito:
Agora podemos ir ao próximo passo e utilizar essas propriedades nas relações que eu te mostrei no Passo 1.
Passo 3
Pra finalizar a questão, vamos montar as equações que vamos utilizar pra plotar um gráfico com as três leis que eu te mostrei no Passo 1.
Vale ressaltar que seria muito completo fazer um gráfico de por com a Lei da parede de Spalding, então nós devemos fazer relações com a equações que te mostrei lá no comecinho.
Bora lá!
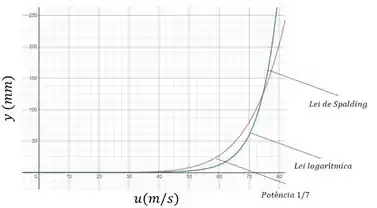
Agora podemos ir no site Desmos e traçar três curvas diferentes com as expressões que acabamos de montar. Vamos varia a velocidade de a , obtendo o gráfico abaixo:
Como a gente pode ver na imagem, as três equações dão resultados muito aproximados para essa faixa de velocidades, inclusive com a lei logarítmica e a lei de Spalding se sobrepondo uma outra, com curvas exatamente iguais.
Pronto, matamos a questão juntos!
Resposta
Os perfis de velocidade por altura na camada limite do escoamento turbulento de ar a em uma placa plana utilizando as leis da potência um sétimo, logarítimica e da parede de Spalding são dados pela figura:
