Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 11
Um líquido incompressível, com massa específica igual a 1250 kg/m3 e viscosidade desprezível, escoa em regime permanente através de um tubo horizontal de diâmetro constante. Em uma seção porosa de comprimento L = 5 m, líquido é removido a uma taxa constante por unidade de comprimento de tal forma que a velocidade uniforme axial no tubo é u(x) = U(1 - x/L), em que U = 15 m/s. Desenvolva expressões para a aceleração de uma partícula fluida ao longo da linha de centro da seção porosa e para o gradiente de pressão ao longo desta linha. Avalie a pressão de saída se a pressão na entrada da seção porosa for igual a 100 kPa (manométrica).
Passo 1
Pessoal, neste caso temos um escoamento em regime permanente apenas na direção x. Desta forma, para a aceleração podemos usar a equação 5.11a do livro:
Como temos apenas escoamento na direção x e em regime permanente, a expressão simplifica para:
Pelo enunciado, sabemos que a velocidade é dada pela expressão:
Portanto, substituindo na equação da aceleração, temos:
Passo 2
Com o mesmo raciocínio usado no item anterior, o gradiente de pressão na linha vai se resumir a direção x. Com isso, podemos usar a expressão 6.2a do livro para representar o gradiente:
Como temos apenas escoamento na direção x e em regime permanente, a expressão simplifica para:
Porém encontramos a seguinte relação no item anterior:
Substituindo, temos:
Para encontrar a pressão basta integrar a expressão acima:
Passo 3
Nesta etapa vamos substituir os valores do enunciado na expressão acima para encontrar a pressão de saída (quando x=L):
Passo 4
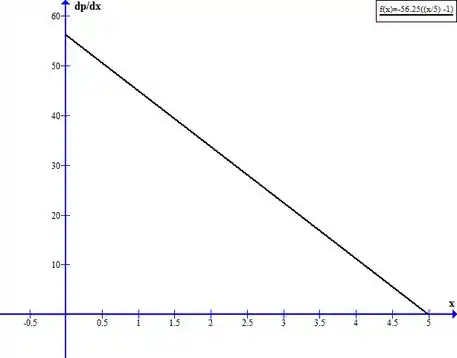
Vamos traçar um gráfico do gradiente de pressão. Pela expressão encontrada no passo 2:
Substituindo os valores do enunciado, temos:
