Um bocal para um fluido incompressível e invíscido, com massa específica ρ = 1000 kg/m3, consiste em uma seção de tubo convergente. Na entrada, o diâmetro é De = 100 mm e, na saída, o diâmetro é Ds = 20 mm. O comprimento do difusor é L = 500 mm e o diâmetro decresce linearmente com a distância x ao longo do bocal. Deduza e trace um gráfico da aceleração de uma partícula fluida considerando escoamento uniforme em cada seção, se a velocidade na entrada for Ve = 1 m/s. Trace um gráfico do gradiente de pressão ao longo do bocal e determine seu valor máximo absoluto. Qual deve ser o comprimento do bocal de modo que o gradiente de pressão não ultrapasse 5 MPa/m em valor absoluto?

A equação do da vazão é dada por:

A velocidade do fluido na entrada é dada então podemos escrever a vazão como:

O enunciado fala que o diâmetro do tubo varia linearmente de ao longo de . Veja o desenho representando:

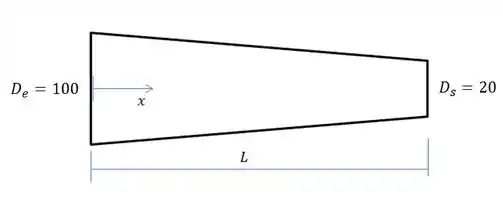
Podemos escrever o diâmetro matematicamente a área em função da distância x:

A vazão pode ser representada na forma geral por:

Onde:

Relacionando as equações de vazão, temos:

No passo 1 encontramos a expressão da aceleração.

Substituindo o valor de encontrado no passo 2:

Vamos trabalhar na derivada:

Vamos fazer a substituição:

Então:

Voltando com os valores originais:

Jogando na expressão toda:

Como:

Para encontrar o gradiente de pressão vamos usar a equação de Euler 6.2a do livro:

Pela equação da aceleração do Passo 1, podemos simplificar a expressão acima:

O gradiente de pressão é dado então por:

Como:

Para a pressão de entrada:

Para a pressão de saída:

Valor máximo absoluto dentro do intervalo.

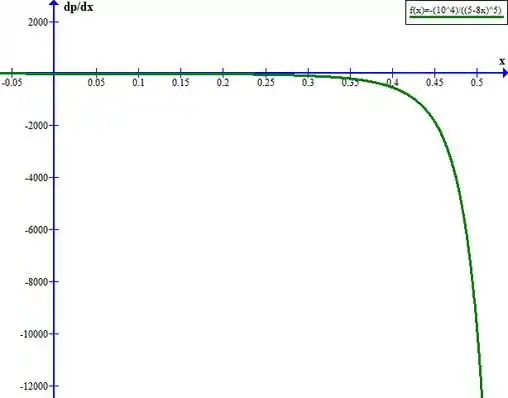
O enunciado pede o comprimento do bocal para que o gradiente de pressão não ultrapasse 5MPa/m em valor absoluto. Então:

Pelo comportamento da expressão, temos que o gradiente é máximo quando

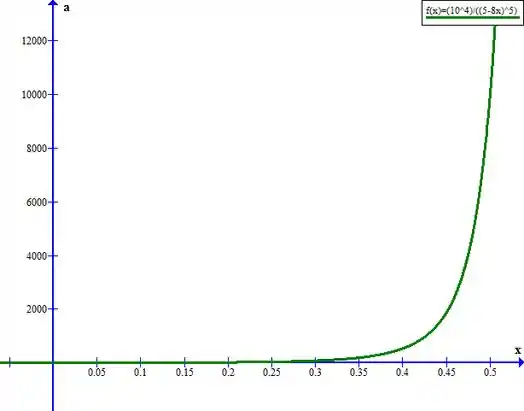
Vamos agora plotar os gráficos pedidos no exercício.

Aceleração:

Gradiente de pressão: