Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 12.Problemas - Ex. 35
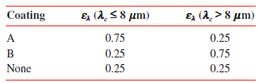
35 – Um de dois revestimentos finos podem ser aplicados em uma placa metálica, produzindo as emissividades espectrais seguintes, abaixo e acima do comprimento de onda de corte, λc = 8 μm.
Se a temperatura da placa é Ts = 600 K e a temperatura da vizinhança é Tviz = 400 K, determine a radiosidade e o fluxo de calor liquido na superfície da placa sem revestimento, com revestimento A, e com revestimento B. Qual revestimento promove o maior fluxo de calor? Se o comprimento de onda de corte for λc = 6 μm ao invés de 8 μm, qual revestimento promove o maior fluxo de calor liquido?
Passo 1
Vamos começar determinando uma expressão para a radiosidade.
A radiosidade pode ser determinada pela soma entre a potência da radiação emitida com a potência da radiação refletida
Onde, E pode ser expressa em termos da potência emitida de um corpo negro:
A potência de radiação refletida pode ser expressa em termos da absortividade, α e da potência de radiação refletida de um corpo negro:
Sendo que a potência emitida de um corpo negro é dada por:
Onde, σ é a constante de Stefan-Boltzmann:
Assim,
Passo 2
Vamos agora determinar expressões para a emissividade e absortividade.
Pela eq. 12.34 do Incropera, a emissividade, ε, pode ser expressa como:
Onde, ε1 e ε2 são, respectivamente, a emissividade para um comprimento de onda abaixo do comprimento de onda de corte e a emissividade para um comprimento de onda acima do comprimento de onda de corte.
O valor de F pode ser encontrado na Tabela 12.2 do Incropera e depende da temperatura da superfície, Ts, e do comprimento de onda.
Analogamente, a absortividade pode ser determinada pela eq. 12.53 o que pode ser expressa de forma análoga para a emissividade:
Mas, agora para a absortividade, o valor de F é determinado pela temperatura da vizinhança, Tviz.
Passo 3
Vamos encontras os valores de F para as duas temperaturas de 400 K e 600 K:
A Tviz = 400 K:
Assim, pela Tabela 12.2:
A Ts = 600 K:
Assim, pela Tabela 12.2:
Passo 4
Vamos agora aos cálculos para cada caso:
-Revestimento A:
Calculando a emissividade:
Calculando a absortividade:
Calculando a radiosidade:
O fluxo de calor liquido é dado pela diferença entre a radiação refletida pela radiosidade, assim
Onde
Assim,
Passo 5
-Revestimento B:
Calculando a emissividade:
Calculando a absortividade:
Calculando a radiosidade:
O fluxo líquido:
Passo 6
-Sem Revestimento:
Calculando a emissividade:
Calculando a absortividade:
Calculando a radiosidade:
O fluxo líquido:
Passo 7
Agora vamos comparar os resultados e verificar qual situação de revestimento que promove o maior fluxo de calor. Analisando comparativamente, você vai ver que o maior fluxo de calor é para o revestimento A, com um fluxo de:
Passo 8
Agora vamos determinar para o caso onde λc = 6 μm. Os cálculos serão os mesmos, modificando os valores começando pelo fator F
Analogamente,
A Tviz = 400 K:
Pela Tabela 12.2:
A Ts = 600 K:
Pela Tabela 12.2:
Passo 9
Para cada caso:
-Revestimento A:
Calculando a emissividade:
Calculando a absortividade:
Calculando a radiosidade:
O fluxo de calor:
Passo 10
-Revestimento B:
Calculando a emissividade:
Calculando a absortividade:
Calculando a radiosidade:
O fluxo líquido:
Passo 11
-Sem Revestimento:
Calculando a emissividade:
Calculando a absortividade:
Calculando a radiosidade:
O fluxo líquido:
Passo 12
O maior fluxo de calor será para o revestimento B para um comprimento de onda de λc = 6 μm.
Resposta
Para λc = 8 μm:
-Revestimento A:
-Revestimento B:
-Sem Revestimento:
Para λc = 6 μm:
-Revestimento A:
-Revestimento B:
-Sem Revestimento: