Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 12.Problemas - Ex. 29
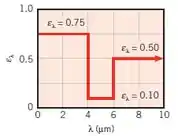
29 – Considere a superfície difusiva do Problema 12.28. Determine a emissividade da superfície hemisférica e a potência emitida em T = 300, 500, e 700 K. Em qual comprimento de onda o pico espectral de emissão ocorre quando a superfície esta nestas temperaturas?
Passo 1
Vamos começar encontrando uma expressão calcularmos a emissividade da superfície e também a potência emitida.
Pela eq. 12.34 do Incropera, a emissividade, ε, pode ser expressa como:
Onde,
Os valores de F são encontrados na Tabela 12.2 do Incropera.
A potência total emitida pode ser determinada pela eq. 13.37 do Incropera:
Onde, Eb é a potência emitida de um corpo negro que é dado pela seguinte expressão:
Onde, σ é a constante de Stefan-Boltzmann
Assim,
Passo 2
Vamos agora aos cálculos para cada temperatura:
Para T = 300 K:
Assim, pela Tabela 12.2:
Calculando a emissividade:
Para a potência total:
Passo 3
Para T = 500 K:
Assim, pela Tabela 12.2:
Calculando a emissividade:
Para a potência total:
Passo 4
Para T = 700 K:
Assim, pela Tabela 12.2:
Calculando a emissividade:
Para a potência total: