53 – Uma chapa de aço emergindo de uma seção de laminação a quente tem uma temperatura de 1000 K, uma espessura de δ = 2,5 mm, e a seguinte distribuição de emissividade hemisférica espectral:
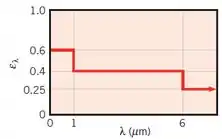
A densidade e o calor especifico do aço são 7900 kg/m3 e 640 J/kg.K, respectivamente. Qual é a emissividade total? Contando para a emissão de ambos os lados da chapa de aço e negligenciando a condução, convecção e a radiação do meio externo, determine a taxa temporal inicial da mudança de temperatura da chapa (dT/dt)i. Como o aço esfria, ele oxida e a emissividade total aumenta. Se este aumento pode ser correlacionado por uma expressão da forma
Quanto tempo vai demorar para o aço resfriar de 1000 K para 500 K?
Passo 1
Vamos começar este exercício determinando a emissividade total.
Para a emissividade total, você pode ver que temos uma emissividade que varia com o comprimento de onda, ou seja, possui uma emissividade para cada largura de banda.
Para calcularmos a emissividade total, então, podemos usar a eq. 12.34 do Incropera, que para esse caso podemos escrever a expressão para emissividade total da seguinte maneira:
Onde,
Os valores de F são encontrados na Tabela 12.2 do Incropera.
Passo 2
Encontrando os valores de F:
A T = 1000 K:
Calculando a emissividade total, aplicando os valores:
Passo 3
Para determinarmos a taxa temporal da mudança de temperatura da chapa, vamos ter que aplicar um balanço de energia na chapa, considerando um processo em regime transiente e desprezando as variações de energia cinética e potencial, além de desprezar as contribuições das energias térmicas já mencionadas no enunciado. Além disso, não teremos também trabalho envolvido neste processo, assim o balanço de energia vai ficar como a energia acumulada na chapa é igual ao calor transferido, que neste caso será o calor transferido por radiação devido a emissividade da chapa.
Assim,
Onde, o sinal negativo representa que a chapa está perdendo energia, isto é, ela está resfriando, como é o caso deste processo.
Passo 4
A energia que sai da chapa, Esai, será a potência de emissividade, contabilizada nos dois lados das superfícies da chapa, assim
A potência total emitida, E, pode ser determinada pela eq. 13.37 do Incropera:
Onde, Eb é a potência emitida de um corpo negro que é dado pela seguinte expressão:
Onde, σ é a constante de Stefan-Boltzmann
Assim,
Logo,
Passo 5
A taxa de variação de energia, dE/dt, pode ser expressão como:
Onde, ρ é a densidade, c é o calor especifico e δ é a espessura.
Assim, o balanço de energia agora é:
Isolando dT/dt:
Passo 6
A taxa inicial então se aplica quando a temperatura é a temperatura inicial que é T = 1000 K, assim, aplicando os valores:
Passo 7
Agora vamos responder a última pergunta. Para determinarmos o tempo requerido para a temperatura da chapa reduzir-se para uma temperatura de 500 K, podemos usar o balanço de energia que já definimos:
Mas agora com a emissividade variando com a temperatura:
Onde,
Assim,
Passo 8
A equação anterior é uma equação diferencial ordinária (EDO) e lembrando de métodos de resolução de EDO’s, um método muito usado é o método da separação de variáveis. Usando o método da separação de variáveis:
Integrando em ambos os lados
Definindo os intervalos de integração, para o qual, para a temperatura varia de 1000 K até 500 K, e o tempo de 0 até t, assim
Resolvendo as integrais, vamos ter que
Passo 9
Isolando t:
Aplicando os valores