Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 107

4.107 Uma placa divisora de jato, de borda viva, inserida parcialmente em uma corrente plana de água, produz o padrão de escoamento mostrado. Analise a situação de modo a avaliar θ como uma função de α , na qual 0 ≤ α ≤ 0,5 . Avalie a força necessária para manter a placa divisora no lugar. (Despreze qualquer força de atrito entre a corrente de água e a placa divisora.) Trace um gráfico de ambos, θ e R x , como funções de α .

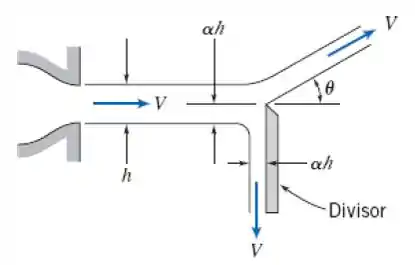
Passo 1

Considerando que a largura seja constante (w) e usando a continuidade.

V w h = V w α h + V w H

h = α h + H

H = h 1 - α

Usando a componente y da equação de quantidade de movimento (desprezando as forças horizontais).

0 = V 2 y ρ V 2 y A 2 + ρ V 3 y A 3

0 = - V ρ V w α h + V   s e n   θ   ρ V w h 1 - α

V   s e n   θ   ρ V w h 1 - α = V ρ V w α h

s e n   θ = α 1 - α

θ = a r c   s e n   α 1 - α

Quando α = 0 , teremos θ = 0 .

Quando α = 0,5 , teremos θ = π 2 e, consequentemente, as duas saídas iguais.

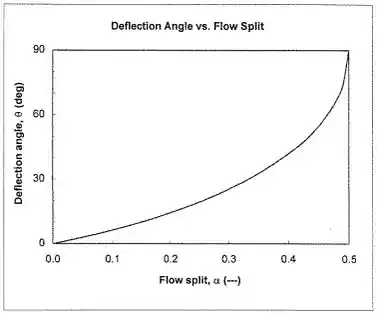
Passo 2

Usando a componente x da equação de quantidade de movimento.

R x = V - ρ V w h + V cos ⁡ θ ρ V w h

R x = ρ V 2 w h - 1 + cos ⁡ θ

Mas sabemos que:

s e n 2 θ + cos 2 ⁡ θ = 1

α 1 - α 2 + cos 2 ⁡ θ = 1

cos 2 ⁡ θ = 1 - α 1 - α 2

cos ⁡ θ = 1 - α 1 - α 2

Então:

R x = ρ V 2 w h - 1 + 1 - α 1 - α 2

Resposta

θ = a r c   s e n   α 1 - α

R x = ρ V 2 w h - 1 + 1 - α 1 - α 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a configuração do jato vertical atingindo o disco vertical conforme mostrado no Problema 4.158 . Suponha que o disco seja largado do repouso a uma altura inicial de 2m acima do plano de saíd
Um pequeno motor de foguete é utilizado para acionar um dispositivo a “jato portátil” destinado a elevar um só astronauta acima da superfície da Lua. O motor do foguete produz um jato uniforme com vel
O tanque móvel mostrado deve ser desacelerado pelo abaixamento de uma concha que capta água de um reservatório. A massa e a velocidade iniciais do tanque, com seu conteúdo, são m 0 e u 0 , respectivam
Deseja-se uma bomba que, acoplada a um motor de 3450 rpm, produza uma altura manométrica teórica de 80 m. O ângulo de entrada das pás deve ser de 15º e o de saída, de 30º. Sendo d 1 = 10c m , quanto d
Uma bomba centrífuga tem pás com ângulo de entrada 15º e de saída de 25º. A rotação é 1720 rpm e os diâmetros de entrada e saída são, respectivamente, de 10cm e 25cm. Sendo v u 1 = 0 e v r 1 = v r 2 ,