Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 10.Exercício - Ex. 12
Deseja-se uma bomba que, acoplada a um motor de 3450 rpm, produza uma altura manométrica teórica de 80 m. O ângulo de entrada das pás deve ser de 15º e o de saída, de 30º. Sendo quanto deve ser , supondo e
Passo 1
Podemos calcular a altura manométrica pela equação:
Como estamos tratando de uma aplicação em bombas podemos utilizar asa hipóteses:
- Regime permanente
- Fluido incompressível
- Pás infinitas
- Sem atritos
- O ângulo de entrada é:
- O ângulo de saída é:
- O diâmetro da entrada:
- A rotação é:
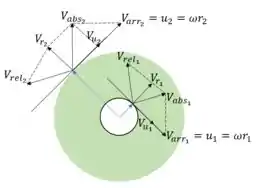
Passo 2
Na entrada temos:
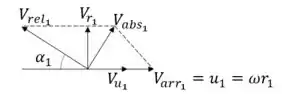
Como
Podemos calcular por sua relação com a rotação:
Utilizando as relações de triângulo podemos
Passo 3
Na saída temos:
Já sabemos que:
Passo 4
Podemos relacionar a velocidade com a rotação
O diâmetro nominal mais próximo é:
Resposta
Exercícios de Livros Relacionados
Reconsidere o helicóptero do Problema 6-34, exceto que ele flutua no alto de uma montanha de 3000m de altitude na qual a densidade do ar é 0,79k g / m 3 . Observando que as pás do helicóptero descarre
As grandes turbinas eólicas disponíveis comercialmente incluem diâmetros de até 100m e geram mais de 3M W de energia elétrica em condições ótimas de projeto. Considere uma turbina eólica com envergadu
Expresse a equação do momento angular em regime não permanente na forma vetorial para um volume de controle que tem um momento constante de inércia I , nenhum torque aplicado, uma corrente de escoamen
Como a equação do momento angular é obtida das equações de transporte de Reynolds?
Um helicóptero sem car ga de massa 10.000k g flutua ao nível do mar enquanto é carregado. No modo de flutuação sem carga, as pás giram a 400r p m . As pás horizontais acima do helicóptero fazem com qu