Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 51
51. A parede, com 150 mm de espessura, de um forno a fogo direto é construída com tijolos de argila refratária (k = 1,5 W/(m · K), ρ = 2600 kg/m3, cp =1000 J/(kg · K)) e está isolada em sua superfície externa. A parede está a uma temperatura inicial uniforme de 20°C, quando os queimadores são acesos e a superfície interna é exposta aos produtos de combustão, para os
quais T∞ = 950°C e h = 100 W/(m2 · K).
(a) Quanto tempo demora para a superfície externa da parede atingir uma temperatura de 750°C?
(b) Represente graficamente a distribuição de temperaturas no interior da parede no tempo determinado no item (a), assim como em diversos tempos intermediários.
Passo 1
Letra (a)
Primeiro Calcule o número do Biot dado por:
Portanto, o método da capacitância concentrada não deve ser aplicado.
Obtenha os valores dos coeficientes e da tabela 5.1 (coeficientes usados na aproximação de um termo às soluções em série para condução unidimensional transitória) no número de Biot .
Considere a relação para difusividade térmica.
Escreva uma expressão matemática para a forma adimensional da distribuição de temperatura.
Substituindo o que nós temos até agora em (1):
Calcule o tempo necessário para a superfície externa atingir a partir da equação (2).
Portanto, o tempo necessário para a superfície externa da parede alcançar será .
Passo 2
Letra (b)
Da equação (2),
Escreva uma expressão para a distribuição de temperatura de cada vez em relação à localização dentro da parede com a ajuda da equação (2).
Em , a equação acima (2) se reduz a,
Em , a equação acima (2) se reduz a,
Em , a equação acima (2) se reduz a,
Desenhe uma tabela para os valores da temperatura em um local diferente dentro da parede, correspondente aos diferentes momentos específicos para os quais as expressões para variação de temperatura são derivadas acima.
Traçar a distribuição de temperatura na parede no momento anterior, bem como vários locais intermediários dentro da parede.
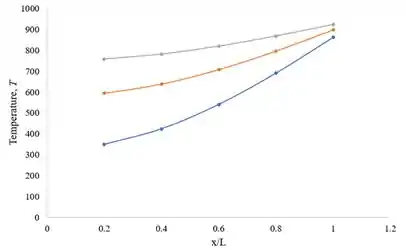
Resposta
- Figura