Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 53

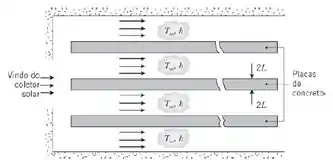
53. Placas de concreto (com pedras misturadas) são usadas para absorver energia térmica a partir de um escoamento de ar oriundo de um grande coletor solar concentrador. As placas são aquecidas durante o dia e liberam sua energia para o ar frio durante a noite. Se o escoamento durante o dia for caracterizado por uma temperatura e um coeficiente de transferência de calor T∞ = 200°C e h = 35 W/(m2 · K), respectivamente, determine a espessura da placa 2L necessária para transferir uma quantidade total de energia tal que Q/Qo = 0,90 em um período de t = 8 h. A temperatura inicial do concreto é Ti = 40°C.

Passo 1

Obtenha as propriedades do concreto na Tabela A.3 em  300 K .

A densidade do concreto:

ρ = 2300   k g / m 3

O calor específico do concreto:

c = 880 J K g . K

A condutividade térmica do concreto:

k = 1,4 W m . K

Considere a relação entre a energia total transferida das superfícies isotérmicas de um plano e a energia total transferida para o interior da parede do avião.

Q Q 0 = 1 - sin ⁡ ξ 1 ξ 1 θ 0 * = 0,9   ( 1 )

Considere a relação para a temperatura da linha central e o número de Fourier.

θ 0 * = C 1 exp ⁡ ( - ξ 1 2 F 0 )     ( 2 )

Considere a relação entre os coeficientes  C 1 ,  ξ 1 para as paredes planas e o número de Biot:

ξ 1 tan ⁡ ξ 1 = B i       ( 3 )

Considere a equação para o valor de  C 1 .

C 1 = 4 sin ⁡ ξ 1 2 ξ 1 + sin ⁡ ( 2 ξ 1 )       ( 4 )

Escreva a relação entre o número Biot e o coeficiente de transferência de calor por convecção local.

B i = h L k     ( 5 )

Escreva a relação entre o número de Fourier e a difusividade térmica.

F 0 = α t L 2

Calcule a difusividade térmica usando a relação,

α = k ρ c

α = 1,4 2300 × 880

= 6,92 × 10 - 7   m 2 / s

Assuma o coeficiente  ξ 1 .

ξ 1 = 1   r a d = 57,29 °

.

Substitua  57,29 °   por  ξ 1   na equação (1).

1 - sin ⁡ ξ 1 ξ 1 θ 0 * = 0,9

1 - sin ⁡ 57,29 ° 1 θ 0 * = 0,9

θ 0 * = 0,119

Substitua  57,29 °   por  ξ 1   na equação (4).

C 1 = 4 sin ⁡ ξ 1 2 ξ 1 + sin ⁡ 2 ξ 1      

C 1 = 4 sin ⁡ 57,29 °   2 × 1 + sin ⁡ ( 2 × 57,29 °   )      

C 1 = 1,16

Passo 2

Substitua  1   r a d   por  ξ 1   na equação (3).

1 × tan ⁡ ( 1 × 57,29 ° ) = B i      

B i = 1,55

B i = h L k

L = B i k h

= 1,4 × 1,55 35

= 0,062   m

Calcular a espessura da parede.

2 L = 2 × 0,062   m

= 0,124   m

Substitua  1 r a d   por  ξ 1 ,  1,16   por  C 1   e 0,119 por  θ 0 * na equação (2).

θ 0 * = C 1 exp ⁡ ( - ξ 1 2 F 0 )

0,119 = 1,16 exp ⁡ ( - 1 r a d 2 F 0 )

F 0 = 2,28

A espessura da parede plana é muito baixa.

Suponha outro coeficiente de valor  ξ 1 .

ξ 1 = 1,1925   r a d = 68,32 °

Substitua  68,32 °   por  ξ 1   na equação (1).

1 - sin ⁡ ξ 1 ξ 1 θ 0 * = 0,9

1 - sin ⁡ 68,32 ° 1,1925 θ 0 * = 0,9

θ 0 * = 0,128

Substitua  1,1925   r a d   por  ξ 1   na equação (4).

C 1 = 4 sin ⁡ ξ 1 2 ξ 1 + sin ⁡ 2 ξ 1      

C 1 = 4 sin ⁡ ( 1,1925   r a d × 57,29 ° )   2 × ( 1,1925   r a d ) + sin ⁡ ( 2 × 1,1925   r a d × 57,29 °   )      

C 1 = 1,2102

Substitua  1 , 1925   r a d   por  ξ 1 ,  1,2102   por  C 1   e 0,128 por  θ 0 * na equação (2).

θ 0 * = C 1 exp ⁡ ( - ξ 1 2 F 0 )

0,128   = 1,2102 exp ⁡ ( - 1,1925 2 F 0 )

F 0 = 1,57

Substituo  1,1925   r a d     por  ξ 1   na equação (3).

1,1925   × tan ⁡ ( 1,1925   × 57,29 ° ) = B i      

B i = 3,00

B i = h L k

L = B i k h

= 1,4 × 3,00 35

= 0,12   m

Calcular a espessura da parede.

2 L = 2 × 0,12   m

= 0,24   m

Assim, a espessura da laje necessária para transferir uma quantidade total de energia tal que,  Q Q 0   = 0,9   durante um período de tempo de 8 horas, tem de ser  0,24   m .

Assim, a aproximação da capacitância concentrada não é apropriada e a aproximação do primeiro termo é válida.

Resposta

2 L = 0,24   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas esferas, A e B , inicialmente a 800K , são subitamente submersas em grandes banhos, que são mantidos à mesma temperatura constante de 320K . Os parâmetros a seguir estão associados a cada uma das
Em um processo de fabricação, longos bastões de diferentes diâmetros estão a uma temperatura uniforme de 400°C no interior de um forno de cura, do qual são retirados e resfriados por convecção forçada
A massa específica e o calor específico de um determinado material são conhecidos ( ρ=1200k g / m 3 ,c p = 1250J / ( k g·K ) ) , mas a sua condutividade térmica é desconhecida. Para determinar a condu
Bilhas de aço inoxidável (AISI 304), que foram aquecidas uniformemente até 850°C, são endurecidas pelo resfriamento em um banho de óleo mantido a 40°C. O diâmetro de cada esfera é de 20 mm e o coefici
Uma esfera de vidro cal-soda de diâmetro D 1=25m m é encapsulada em uma casca esférica de baquelita de espessura L=10m m . A esfera composta está inicialmente a uma temperatura uniforme, T i = 40 ° C