Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 69
A massa específica e o calor específico de um determinado material são conhecidos ( mas a sua condutividade térmica é desconhecida. Para determinar a condutividade térmica, um longo cilindro do material com diâmetro é torneado e um termopar é inserido através de um pequeno furo ao longo de seu eixo central.
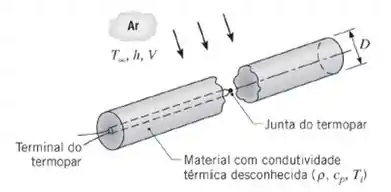
A condutividade térmica é determinada realizando-se um experimento no qual o cilindro é aquecido até uma temperatura uniforme Ti = 100°C e, então, resfriado pela passagem de ar a T∞ = 25°C em escoamento cruzado sobre o cilindro. Para a velocidade do ar especificada, o coeficiente convectivo é de
(a) Se uma temperatura no eixo central de T(0, t) = 40°C for registrada após t = 1136 s de resfriamento, verifique que o material tem uma condutividade térmica de k = 0,30 W/(m · K).
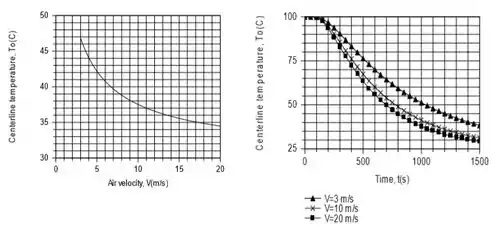
(b) Para o ar em escoamento cruzado sobre o cilindro, o valor especificado de h = 55 W/(m2 · K) corresponde a uma velocidade de V = 6,8 m/s. Se h = CV0,618, estando a constante C com unidades de W · s0,618/(m2,618 · K), como a temperatura no eixo central em t = 1136 s varia com a velocidade para 3 ≤ V ≤ 20 m/s? Determine os históricos da temperatura no eixo central para 0 ≤ t ≤ 1500 s e velocidades de 3, 10 e 20 m/s.
Passo 1
Vamo lá galera! (a) Com,
Da equação 5.52c temos:
Logo,
Passo 2
Com , as variações desejadas de temperatura da linha central com velocidade (para t = 1136 s) e tempo (para V = 3, 10 e 20 m/s) são as seguintes:
