Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 77
Duas esferas, e , inicialmente a , são subitamente submersas em grandes banhos, que são mantidos à mesma temperatura constante de . Os parâmetros a seguir estão associados a cada uma das esferas e aos seus respectivos processos de resfriamento.
(a) Mostre de maneira qualitativa, em coordenadas , as temperaturas no centro e na superfície de cada esfera em função do tempo. Explique sucintamente o raciocínio utilizado na determinação do posicionamento relativo das duas curvas.
(b) Calcule o tempo necessário para a superfície de cada esfera atingir .
(c) Determine a energia ganha por cada um dos banhos durante o processo de resfriamento das esferas até a temperatura superficial de .
Passo 1
Vamos lá! Nosso problema nos pede o tempo necessário para a remoção de para atingir a temperatura de a energia cedida e os gráficos , mas antes que tal desenharmos um esboço do comportamento desse problema pra entendermos o que o ocorre. Fica assim.
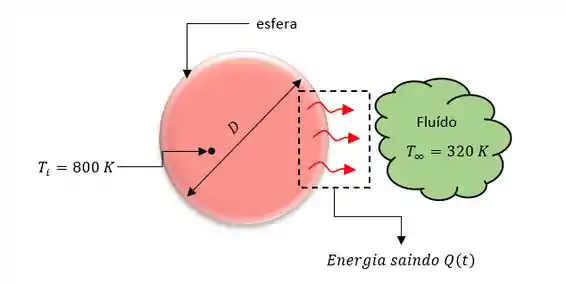
Agora vamos as nossas famosas considerações pra resolver nosso problema.
Passo 2
(a)
Para avaliarmos qualitativamente o gráfico da temperatura tempo, precisamos do número de e a constante de tempo térmica, provenientes das equações 5.10 e , para o número de fica:
Disso temos que para a esfera podemos usar a consideração da capacitância global o que nos indica que ela é espacialmente isotérmica, já pra esfera teremos que fazer uma análise especifica para cada seção da esfera segundo as equações e , como vamos fazer isso na letra (b) e (c), somente ilustraremos o gráfico de acordo com a constante de tempo térmica.
Agora usando a constante de tempo térmica para ambas as situações temos:
Como , isso nos indica que a esfera ira perder calor de forma mais intensa, assim nosso gráfico fica:
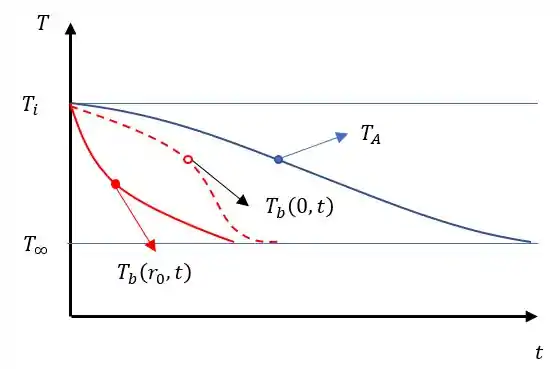
Passo 3
(b)
Como a esfera é isotérmica espacialmente usando a equação e :
Aplicando o temos:
Como havíamos discutido antes como temos que tratar cada caso com particularidade, assim temos:
Da tabela temos e assim lembrando que da equação , temos:
Como representa a variação térmica adimensional temos:
Substituindo na equação 5.53 temos:
Por fim temos que , assim:
Passo 4
(c)
Para a esfera o balanço de energia é dado por:
Como havíamos discutido antes como temos que tratar cada caso com particularidade, assim temos:
Da tabela temos e assim temos:
Lembrando que da equação , temos:
Sendo , substituindo isso na equação temos:
Ufa, finalmente terminamos!
Normalmente é bom tomar cuidado com esse tipo de questão porque alguns professores gostam de colocar em prova, mas é só tentar manter tudo organizado para não errarmos com bobagens ao longo da questão!
Resposta
(b)
(c)